Kimberling’s point X(26)

CIRCUMCENTER OF THE TANGENTIAL TRIANGLE X(26)

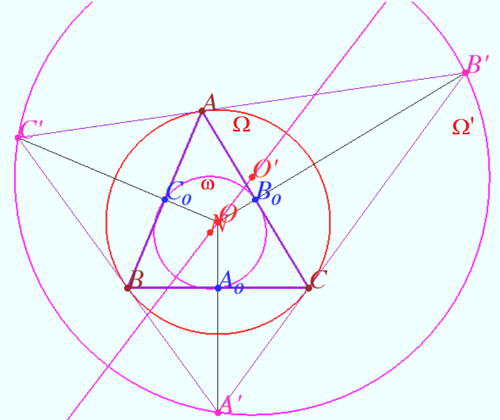
The circumcenter of the tangential triangle $\triangle A'B'C'$ of $\triangle ABC$ (Kimberling’s point $X(26))$ lies on the Euler line of $\triangle ABC$ (The tangential triangle of a reference triangle (other than a right triangle) is the triangle whose sides are on the tangent lines to the reference triangle's circumcircle at the reference triangle's vertices).

Proof

Let $A_0, B_0,$ and $C_0$ be midpoints of $BC, AC,$ and $AB,$ respectively.

Let $\omega$ be circumcircle of $\triangle A_0B_0C_0.$ It is nine-points circle of the $\triangle ABC.$

Let $\Omega$ be circumcircle of $\triangle ABC.$ Let $\Omega'$ be circumcircle of $\triangle A'B'C'.$

$A'B$ and $A'C$ are tangents to $\Omega \implies$ inversion with respect $\Omega$ swap $B'$ and $B_0.$ Similarly, this inversion swap $A'$ and $A_0, C'$ and $C_0.$

Therefore this inversion swap $\omega$ and $\Omega'.$ The center $N$ of $\omega$ and the center $O$ of $\Omega$ lies on Euler line, so the center $O'$ of $\Omega'$ lies on this line, as desired.

After some calculations in the case, shown on diagram, we can get

$OO'= \frac {2R}{t^{–1}–t},$ where $t = \sqrt {9 – \frac{a^2 +b^2 + c^2}{R^2}}, R = OA, a = BC, b = AC, c = AB.$

Similarly, one can find position of point $X(26)$ on Euler line in another cases.

vladimir.shelomovskii@gmail.com, vvsss

Page

Toolbox

Search

Kimberling’s point X(26)

CIRCUMCENTER OF THE TANGENTIAL TRIANGLE X(26)