Kimberling’s point X(23)
Far-out point X(23)
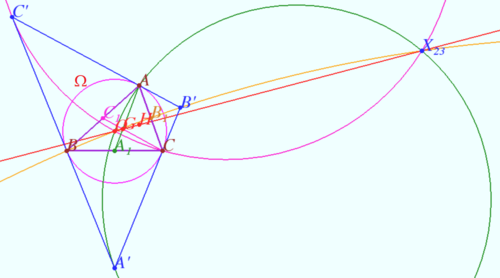
Let ![]() be the tangential triangle of
be the tangential triangle of ![]()
Let ![]() and
and ![]() be the centroid, circumcircle, circumcenter, circumradius and orthocenter of
be the centroid, circumcircle, circumcenter, circumradius and orthocenter of ![]()
Prove that the second crosspoint of circumcircles of ![]() and
and ![]() is point
is point ![]() Point
Point ![]() lies on Euler line of
lies on Euler line of ![]()
Proof
Denote ![]() the inversion with respect
the inversion with respect ![]() midpoints of
midpoints of ![]()
It is evident that ![]()
The inversion of circles ![]() are lines
are lines ![]() which crosses at point
which crosses at point ![]()
Therefore point ![]() lies on Euler line
lies on Euler line ![]() of
of ![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss









