2017 AMC 10A Problems/Problem 12

Problem

Let $S$ be a set of points $(x,y)$ in the coordinate plane such that two of the three quantities $3,~x+2,$ and $y-4$ are equal and the third of the three quantities is no greater than this common value. Which of the following is a correct description for $S?$

$\textbf{(A)}\ \text{a single point} \qquad\textbf{(B)}\ \text{two intersecting lines} \\\qquad\textbf{(C)}\ \text{three lines whose pairwise intersections are three distinct points} \\\qquad\textbf{(D)}\ \text{a triangle} \qquad\textbf{(E)}\ \text{three rays with a common endpoint}$

Solution 1

If the two equal values are $3$ and $x+2$ , then $x=1$ . Also, $y-4\le 3$ because $3$ is the common value. Solving for $y$ , we get $y \le 7$ . Therefore the portion of the line $x=1$ where $y \le 7$ is part of $S$ . This is a ray with an endpoint of $(1, 7)$ .

Similar to the process above, we assume that the two equal values are $3$ and $y-4$ . Solving the equation $3=y-4$ then $y=7$ . Also, $x+2\le 3$ because 3 is the common value. Solving for $x$ , we get $x\le1$ . Therefore the portion of the line $y=7$ where $x\le 1$ is also part of $S$ . This is another ray with the same endpoint as the above ray: $(1, 7)$ .

If $x+2$ and $y-4$ are the two equal values, then $x+2=y-4$ . Solving the equation for $y$ , we get $y=x+6$ . Also $3\le y-4$ because $y-4$ is one way to express the common value. Solving for $y$ , we get $y\ge 7$ . We also know $3\le x+2$ , so $x\ge 1$ .Therefore the portion of the line $y=x+6$ where $y\ge 7$ is part of $S$ like the other two rays. The lowest possible value that can be achieved is also $(1, 7)$ .

Since $S$ is made up of three rays with common endpoint $(1, 7)$ , the answer is $\boxed{\textbf{(E) }\text{three rays with a common endpoint}}$

Solution 2 (Graphing $S$)

Similar to above, we make three equations.

$ 3 = x + 2 $

$ 3 = y - 4 $

$ x + 2 = y - 4 $

and solve them in terms of a linear equation

$ x = 1 $

$ y = 7 $

$ x + 6 = y $

We proceed to graph each of the three equations.

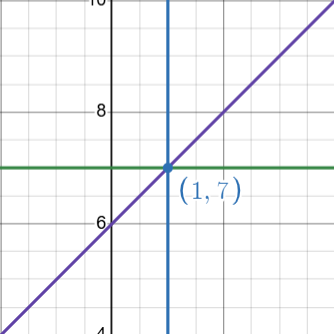
We now see that no third value is less than the common point. Therefore, we want the overlapping region of $ y \ge 7 $ and $ x \ge 1 $.

There are three lines in this region that start at a point $(1, 7)$. A line that extends forever starting at any point is called a ray. Because we have three of these lines, particularly $ x = 1 $, $ y = 7 $, and $ x + 6 = y $, we have $\boxed{\textbf{(E) }\text{three rays with a common endpoint}}$ .

~Pinotation

Video Solution

https://youtu.be/s4vnGlwwHHw?t=190

2017 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 11	Followed by Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

2017 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 8	Followed by Problem 10
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search

2017 AMC 10A Problems/Problem 12

Contents

Problem

Solution 1

Solution 2 (Graphing \(S\))

Video Solution

See Also