Kimberling center
C. Kimberling has extensively tabulated and enumerated the properties of triangle centers (Kimberling 1994, 1998, and online), denoting the nth center in his numbering scheme by 
. 101 (plus 13 additional) centers appeared in Kimberling (1994), 360 in Kimberling (1998), and the remainder appear in a list maintained online by Kimberling at http://faculty.evansville.edu/ck6/encyclopedia/ETC.html. In his honor, these centers are called Kimberling centers in this work. Kimberling's compilation contains 3053 centers as of December 2004. A subset of these is illustrated above.
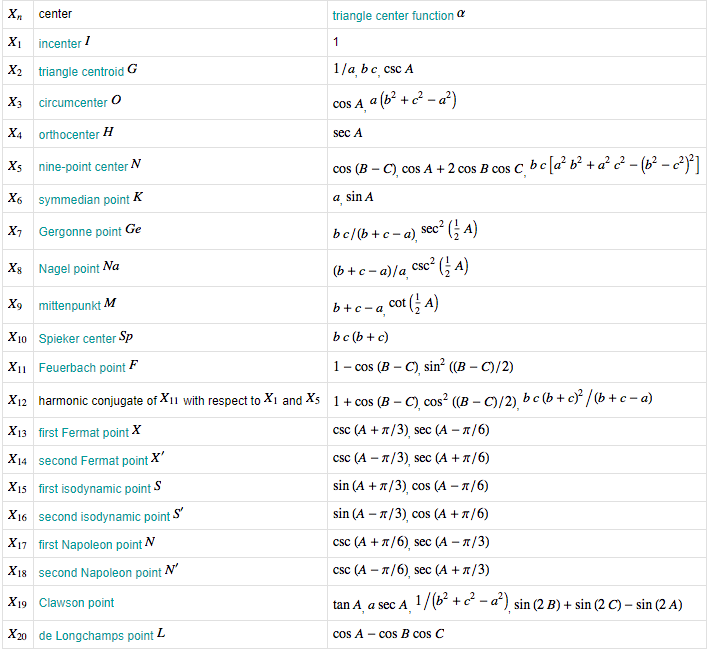
The first few Kimberling centers are summarized in the table below with their numbers, names, and trilinears.
.png)
Weisstein, Eric W. "Kimberling Center." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/KimberlingCenter.html
