Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus
GET READY FOR THE AMC 12 WITH AoPS
Learn with outstanding instructors and top-scoring students from around the world in our AMC 12 Problem Series online course.
CHECK SCHEDULE

2003 AMC 12B Problems

Revision as of 18:08, 1 February 2010 by Eshen (talk | contribs) (→Problem 13)

Problem 1

Which of the following is the same as

\[\frac{2-4+6-8+10-12+14}{3-6+9-12+15-18+21}\]?

$\text {(A) } -1 \qquad \text {(B) } -\frac{2}{3} \qquad \text {(C) } \frac{2}{3} \qquad \text {(D) } 1 \qquad \text {(E) } \frac{14}{3}$

Solution

Problem 2

Solution

Problem 3

Solution

Problem 4

Solution

Problem 5

Solution

Problem 6

Solution

Problem 7

Solution

Problem 8

Solution

Problem 9

Solution

Problem 10

Solution

Problem 11

Solution

Problem 12

Solution

Problem 13

An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly fill the cone. Assume that the melted ice cream occupies $75\%$ of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radius?

$\mathrm{(A)}\ 2:1 \qquad\mathrm{(B)}\ 3:1 \qquad\mathrm{(C)}\ 4:1 \qquad\mathrm{(D)}\ 16:3 \qquad\mathrm{(E)}\ 6:1$

Solution

Problem 14

Solution

Problem 15

Solution

Problem 16

Solution

Problem 17

If $\log (xy^3) = 1$ and $\log (x^2y) = 1$, what is $\log (xy)$?

$\mathrm{(A)}\ -\frac 12 \qquad\mathrm{(B)}\ 0 \qquad\mathrm{(C)}\ \frac 12 \qquad\mathrm{(D)}\ \frac 35 \qquad\mathrm{(E)}\ 1$

Solution

Problem 18

Let $n$ be a 5-digit number, and let q and r be the quotient and remainder, respectively, when $n$ is divided by 100. For how many values of $n$ is $q + r$ divisible by 11?

$\text {(A) } 8180 \qquad \text {(B) } 8181 \qquad \text {(C) } 8182 \qquad \text {(D) } 9000 \qquad \text {(E) } 9090$

Solution

Problem 19

Let $S$ be the set of permutations of the sequence $1,2,3,4,5$ for which the first term is not $1$. A permutation is chosen randomly from $S$. The probability that the second term is $2$, in lowest terms, is $a/b$. What is $a+b$?

$\mathrm{(A)}\ 5 \qquad\mathrm{(B)}\ 6 \qquad\mathrm{(C)}\ 11 \qquad\mathrm{(D)}\ 16 \qquad\mathrm{(E)}\ 19$

Solution

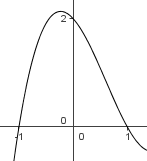
Problem 20

Part of the graph of $f(x) = ax^3 + bx^2 + cx + d$ is shown. What is $b$?

$\mathrm{(A)}\ -4 \qquad\mathrm{(B)}\ -2 \qquad\mathrm{(C)}\ 0 \qquad\mathrm{(D)}\ 2 \qquad\mathrm{(E)}\ 4$

Solution

Problem 21

An object moves $8$ cm in a straight line from $A$ to $B$, turns at an angle $\alpha$, measured in radians and chosen at random from the interval $(0,\pi)$, and moves $5$ cm in a straight line to $C$. What is the probability that $AC < 7$?

$\mathrm{(A)}\ 448 \qquad\mathrm{(B)}\ 486 \qquad\mathrm{(C)}\ 1560 \qquad\mathrm{(D)}\ 2001 \qquad\mathrm{(E)}\ 2003$

Solution

Problem 22

Let $ABCD$ be a rhombus with $AC = 16$ and $BD = 30$. Let $N$ be a point on $\overline{AB}$, and let $P$ and $Q$ be the feet of the perpendiculars from $N$ to $\overline{AC}$ and $\overline{BD}$, respectively. Which of the following is closest to the minimum possible value of $PQ$?

[asy] size(200); defaultpen(0.6); pair O = (15*15/17,8*15/17), C = (17,0), D = (0,0), P = (25.6,19.2), Q = (25.6, 18.5); pair A = 2*O-C, B = 2*O-D; pair P = (A+O)/2, Q=(B+O)/2, N=(A+B)/2; draw(A--B--C--D--cycle); draw(A--O--B--O--C--O--D); draw(P--N--Q); label("\(A\)",A,WNW); label("\(B\)",B,ESE); label("\(C\)",C,ESE); label("\(D\)",D,SW); label("\(P\)",P,SSW); label("\(Q\)",Q,SSE); label("\(N\)",N,NNE); [/asy]

$\mathrm{(A)}\ 6.5 \qquad\mathrm{(B)}\ 6.75 \qquad\mathrm{(C)}\ 7 \qquad\mathrm{(D)}\ 7.25 \qquad\mathrm{(E)}\ 7.5$

Solution

Problem 23

The number of $x$-intercepts on the graph of $y=\sin(1/x)$ in the interval $(0.0001,0.001)$ is closest to

$\mathrm{(A)}\ 2900 \qquad\mathrm{(B)}\ 3000 \qquad\mathrm{(C)}\ 3100 \qquad\mathrm{(D)}\ 3200 \qquad\mathrm{(E)}\ 3300$ Solution

Problem 24

Positive integers $a,b,$ and $c$ are chosen so that $a<b<c$, and the system of equations

$2x + y = 2003 \quad$ and $\quad y = |x-a| + |x-b| + |x-c|$

has exactly one solution. What is the minimum value of $c$?

$\mathrm{(A)}\ 668 \qquad\mathrm{(B)}\ 669 \qquad\mathrm{(C)}\ 1002 \qquad\mathrm{(D)}\ 2003 \qquad\mathrm{(E)}\ 2004$

Solution

Problem 25

Three points are chosen randomly and independently on a circle. What is the probability that all three pairwise distance between the points are less than the radius of the circle?

$\mathrm{(A)}\ \dfrac{1}{36} \qquad\mathrm{(B)}\ \dfrac{1}{24} \qquad\mathrm{(C)}\ \dfrac{1}{18} \qquad\mathrm{(D)}\ \dfrac{1}{12} \qquad\mathrm{(E)}\ \dfrac{1}{9}$

Solution

See also

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2003_AMC_12B_Problems&oldid=33283"