2002 AIME I Problems/Problem 10

Problem

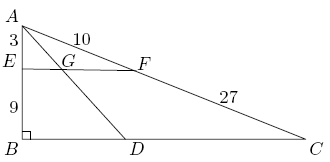
In the diagram below, angle $ABC$ is a right angle. Point $D$ is on $\overline{BC}$ , and $\overline{AD}$ bisects angle $CAB$ . Points $E$ and $F$ are on $\overline{AB}$ and $\overline{AC}$ , respectively, so that $AE=3$ and $AF=10$ . Given that $EB=9$ and $FC=27$ , find the integer closest to the area of quadrilateral $DCFG$ .

Solution

By the Pythagorean Theorem, $BC=35$ . Letting $BD=x$ we can use the angle bisector theorem on triangle ABC to get $x/12=(35-x)/37$ , and solving gives $BD=60/7$ and $DC=185/7$ . Now, the area of triangle AGF is 10/3 that of triangle AEG, since they share a common side an angle, so the area of triangle AGF is 10/13 the area of triangle AEF. Since the area of a triangle is 1/2absinC, the area of AEF is 525/37 and the area of AGF=5250/581. The area of triangle ABD is 360/7. The area of the whole triangle ABC is 210. Subtracting the areas of ABD and AGF from 210 and finding the closest integer gives 148 as the answer.

2002 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 9	Followed by Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

2002 AIME I Problems/Problem 10

Problem

Solution

See also