2018 IMO Problems/Problem 6

A convex quadrilateral $ABCD$ satisfies $AB\cdot CD=BC \cdot DA.$ Point $X$ lies inside $ABCD$ so that $\angle XAB = \angle XCD$ and $\angle XBC = \angle XDA.$ Prove that $\angle BXA + \angle DXC = 180^{\circ}$

Solution

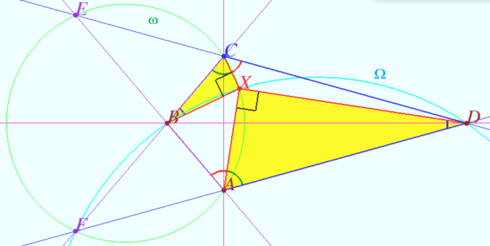
Special case

We construct point $X_0$ and prove that $X_0$ coincides with the point $X.$

Let $AD = CD$ and $AB = BC \implies AB \cdot CD = BC \cdot DA.$

Let $E$ and $F$ be the intersection points of $AB$ and $CD,$ and $BC$ and $DA,$ respectively.

The points $B$ and $D$ are symmetric with respect to the circle $\omega = EACF$ (Claim 1). The circle $\Omega = FBD$ is orthogonal to the circle $\omega$ (Claim 2). Let $X_0$ be the point of intersection of the circles $\omega$ and $\Omega.$ $\angle X_0AB = \angle X_0CD$ (quadrilateral $AX_0CF$ is cyclic) and $\angle X_0BC = \angle X_0DA$ (quadrangle $DX_0BF$ is cyclic). This means that $X_0$ coincides with the point $X$ indicated in the condition.

$\angle FCX = \angle BCX$ subtend the arc $\overset{\Large\frown} {XF}$ of $\omega, \angle CBX = \angle XDA$ subtend the arc $\overset{\Large\frown} {XF}$ of $\Omega.$ The sum of these arcs is $180^\circ$ (Claim 3)..

Hence, the sum of the arcs XF is 180°, the sum of the angles ∠XСВ + ∠XВС = 90°, ∠СХВ = 90°. Similarly, ∠AXD = 90°, that is, ∠BXA + ∠DXC = 180°.

Claim 1

Let A, C, and E be arbitrary points on a circle ω, l be the middle perpendicular to the segment AC. Then the straight lines AE and CE intersect l at the points B and D, symmetric with respect to ω.

Page

Toolbox

Search

2018 IMO Problems/Problem 6

Solution