2021 USAJMO Problems/Problem 2

Problem

Rectangles $BCC_1B_2,$ $CAA_1C_2,$ and $ABB_1A_2$ are erected outside an acute triangle $ABC.$ Suppose that $\angle BC_1C+\angle CA_1A+\angle AB_1B=180^{\circ}.$ Prove that lines $B_1C_2,$ $C_1A_2,$ and $A_1B_2$ are concurrent.

Solution

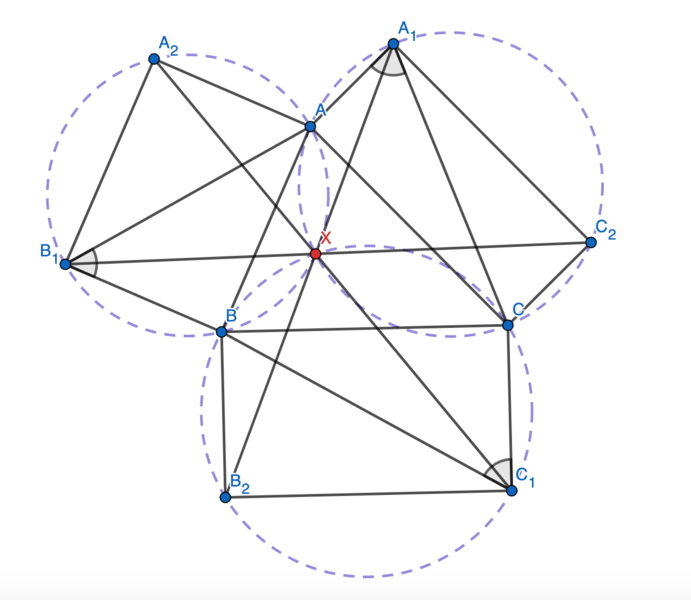
We first claim that the three circles $(BCC_1B_2),$ $(CAA_1C_2),$ and $(ABB_1A_2)$ are share a common intersection.

Let the second intersection of $(BCC_1B_2)$ and $(CAA_1C_2)$ be $K$ . Then $\begin{align*} \angle AKC &= 360^\circ - \angle BKA - \angle CKB \\ &= 360^\circ - (180^\circ - \angle AB_1B + 180^\circ - \angle BC_1C) \\& = 180^\circ - \angle CA_1A, \end{align*}$ which implies that $AA_1C_2CK$ is cyclic as desired.

Now we show that $K$ is the intersection of $B_1C_2,$ $C_1A_2,$ and $A_1B_2.$ Note that $\angle C_1XB = \angle BXA_2 = 90^\circ,$ so $A_2, K, C_1$ are collinear. Similarly, $B_1, K, C_2$ and $A_1, K, B_2$ are collinear, so the three lines concur and we are done.

~Leonard_my_dude

Page

Toolbox

Search

2021 USAJMO Problems/Problem 2

Problem

Solution