MIE 2016/Day 1/Problem 10: Difference between revisions
Created page with "===Problem 10=== A hexagon is divided into 6 equilateral triangles. How many ways can we put the numbers from 1 to 6 in each triangle, without repetition, such that the sum of..." |
|||
| Line 19: | Line 19: | ||
==See Also== | ==See Also== | ||
{{Mie 2016 Day 1 box|year=2016|num-b=9|num-a=11}} | |||
{{MAA Notice}} | |||
Revision as of 21:13, 10 January 2018
Problem 10
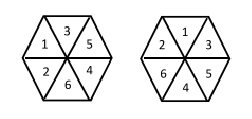
A hexagon is divided into 6 equilateral triangles. How many ways can we put the numbers from 1 to 6 in each triangle, without repetition, such that the sum of the numbers of three adjacent triangles is always a multiple of 3? Solutions obtained by rotation or reflection are differents, thus the following figures represent two distinct solutions.
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(e) ![]()
Solution
See Also
These problems are copyrighted © by the Mathematical Association of America.