2004 AMC 12A Problems/Problem 18: Difference between revisions

Revision as of 13:24, 25 July 2015

The following problem is from both the 2004 AMC 12A #18 and 2004 AMC 10A #22, so both problems redirect to this page.

Problem

Square $ABCD$ has side length $2$ . A semicircle with diameter $\overline{AB}$ is constructed inside the square, and the tangent to the semicircle from $C$ intersects side $\overline{AD}$ at $E$ . What is the length of $\overline{CE}$ ?

$[asy] size(100); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2); draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180)); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); [/asy]$

$\mathrm{(A) \ } \frac{2+\sqrt{5}}{2} \qquad \mathrm{(B) \ } \sqrt{5} \qquad \mathrm{(C) \ } \sqrt{6} \qquad \mathrm{(D) \ } \frac{5}{2} \qquad \mathrm{(E) \ } 5-\sqrt{5}$

Solution 1

$[asy] size(150); defaultpen(fontsize(10)); pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2), F=E+(C-E)/abs(C-E)/2; draw(A--B--C--D--cycle);draw(C--E); draw(Arc((1,0),1,0,180));draw((A+B)/2--F); label("$A$",A,(-1,-1)); label("$B$",B,( 1,-1)); label("$C$",C,( 1, 1)); label("$D$",D,(-1, 1)); label("$E$",E,(-1, 0)); label("$F$",F,( 0, 1)); label("$x$",(A+E)/2,(-1, 0)); label("$x$",(E+F)/2,( 0, 1)); label("$2$",(F+C)/2,( 0, 1)); label("$2$",(D+C)/2,( 0, 1)); label("$2$",(B+C)/2,( 1, 0)); label("$2-x$",(D+E)/2,(-1, 0)); [/asy]$ Let the point of tangency be $F$ . By the Two Tangent Theorem $BC = FC = 2$ and $AE = EF = x$ . Thus $DE = 2-x$ . The Pythagorean Theorem on $\triangle CDE$ yields

$\begin{align*} DE^2 + CD^2 &= CE^2\\ (2-x)^2 + 2^2 &= (2+x)^2\\ x^2 - 4x + 8 &= x^2 + 4x + 4\\ x &= \frac{1}{2}\end{align*}$

Hence $CE = FC + x = \frac{5}{2} \Rightarrow\boxed{\mathrm{(D)}\ \frac{5}{2}}$ .

Solution 2

Clearly, $EA = EF = BG$ . Thus, the sides of right triangle $CDE$ are in arithmetic progression. Thus it is similar to the triangle $3 - 4 - 5$ and since $DC = 2$ , $CE = 5/2$ .

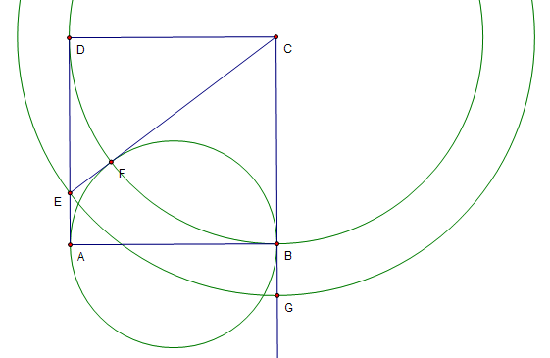
Solution 3

size(150);
defaultpen(fontsize(10));
pair A=(0,0), B=(2,0), C=(2,2), D=(0,2), E=(0,1/2), F=E+(C-E)/abs(C-E)/2;
draw(A--B--C--D--cycle);draw(C--E);draw(
draw(Arc((1,0),1,0,180));draw((A+B)/2--F);
label("$A$",A,(-1,-1));
label("$B$",B,( 1,-1));
label("$C$",C,( 1, 1));
label("$D$",D,(-1, 1));
label("$E$",E,(-1, 0));
label("$F$",F,( 0, 1));
label("$x$",(A+E)/2,(-1, 0));
label("$x$",(E+F)/2,( 0, 1));
label("$2$",(F+C)/2,( 0, 1));
label("$2$",(D+C)/2,( 0, 1));
label("$2$",(B+C)/2,( 1, 0));
label("$O$, (1,0), S);
 (Error making remote request. Unknown error_msg)

2004 AMC 12A (Problems • Answer Key • Resources)
Preceded by Problem 17	Followed by Problem 19
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

2004 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 21	Followed by Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

Page

Toolbox

Search