2003 AMC 12A Problems/Problem 13: Difference between revisions
No edit summary |
|||
| Line 1: | Line 1: | ||
{{duplicate|[[2003 AMC 12A Problems|2003 AMC 12A #13]] and [[2003 AMC 10A Problems|2003 AMC 10A #10]]}} | |||
== Problem == | == Problem == | ||
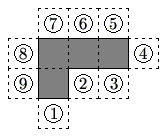
The [[polygon]] enclosed by the solid lines in the figure consists of 4 [[congruent]] [[square (geometry) | squares]] joined [[edge]]-to-edge. One more congruent square is attached to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a [[cube (geometry) | cube]] with one face missing? | The [[polygon]] enclosed by the solid lines in the figure consists of 4 [[congruent]] [[square (geometry) | squares]] joined [[edge]]-to-edge. One more congruent square is attached to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a [[cube (geometry) | cube]] with one face missing? | ||
| Line 7: | Line 8: | ||
== Solution == | == Solution == | ||
[[Image: | ===Solution 1=== | ||
[[Image:2003amc10a10solution.gif]] | |||
Let the squares be labeled <math>A</math>, <math>B</math>, <math>C</math>, and <math>D</math>. | Let the squares be labeled <math>A</math>, <math>B</math>, <math>C</math>, and <math>D</math>. | ||
| Line 19: | Line 21: | ||
Squares <math>4</math>, <math>5</math>, <math>6</math>, <math>7</math>, <math>8</math>, and <math>9</math> will allow the polygon to become a cube with one face missing when folded. | Squares <math>4</math>, <math>5</math>, <math>6</math>, <math>7</math>, <math>8</math>, and <math>9</math> will allow the polygon to become a cube with one face missing when folded. | ||
Thus the answer is <math>6 \ | Thus the answer is <math>\boxed{\mathrm{(E)}\ 6}</math>. | ||
===Solution 2=== | |||
Another way to think of it is that a cube missing one face has <math>5</math> of its <math>6</math> faces. Since the shape has <math>4</math> faces already, we need another face. The only way to add another face is if the added square does not overlap any of the others. <math>1</math>,<math>2</math>, and <math>3</math> overlap, while squares <math>4</math> to <math>9</math> do not. The answer is <math>\boxed{\mathrm{(E)}\ 6}</math> | |||
== See Also == | == See Also == | ||
{{AMC10 box|year=2003|ab=A|num-b=9|num-a=11}} | |||
{{AMC12 box|year=2003|ab=A|num-b=12|num-a=14}} | {{AMC12 box|year=2003|ab=A|num-b=12|num-a=14}} | ||
[[Category:Introductory Geometry Problems]] | [[Category:Introductory Geometry Problems]] | ||
Revision as of 17:21, 31 July 2011
- The following problem is from both the 2003 AMC 12A #13 and 2003 AMC 10A #10, so both problems redirect to this page.
Problem
The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attached to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?
Solution
Solution 1
Let the squares be labeled 
, 
, 
, and 
.
When the polygon is folded, the "right" edge of square becomes adjacent to the "bottom edge" of square , and the "bottom" edge of square becomes adjacent to the "bottom" edge of square .
So, any "new" square that is attatched to those edges will prevent the polygon from becoming a cube with one face missing.
Therefore, squares 
, 
, and 
will prevent the polygon from becoming a cube with one face missing.
Squares 
, 
, 
, 
, 
, and 
will allow the polygon to become a cube with one face missing when folded.
Thus the answer is 
.
Solution 2
Another way to think of it is that a cube missing one face has of its faces. Since the shape has faces already, we need another face. The only way to add another face is if the added square does not overlap any of the others. ,, and overlap, while squares to do not. The answer is
See Also
| 2003 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2003 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 12 |
Followed by Problem 14 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
