2007 AMC 10A Problems/Problem 15: Difference between revisions
m typo |
Arachnotron (talk | contribs) |
||
| Line 10: | Line 10: | ||
<cmath>A=(2+3\sqrt{2})^2=4+6\sqrt{2}+6\sqrt{2}+18=22+12\sqrt{2} \Rightarrow \text{(B)}</cmath> | <cmath>A=(2+3\sqrt{2})^2=4+6\sqrt{2}+6\sqrt{2}+18=22+12\sqrt{2} \Rightarrow \text{(B)}</cmath> | ||
== Alternate Solution == | |||
Extend two radii from the larger circle to the centers of the two smaller circles above (or below -- it's irrelevant). This forms a right triangle of sides <math>3, 3, 3\sqrt{2}</math>. The length of the hypotenuse of the right triangle plus twice the radius of the smaller circle is equal to the side of the square. It follows, then <cmath> A = (2+3\sqrt{2})^2 = 22 + 12\sqrt{2} \Rightarrow \text{(B)}</cmath> | |||
==See Also== | ==See Also== | ||
Revision as of 19:31, 27 November 2008
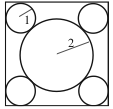
Problem
Four circles of radius 
are each tangent to two sides of a square and externally tangent to a circle of radius 
, as shown. What is the area of the square?
Solution
The diagonal has length 
. Therefore the sides have length 
, and the area is
![\[A=(2+3\sqrt{2})^2=4+6\sqrt{2}+6\sqrt{2}+18=22+12\sqrt{2} \Rightarrow \text{(B)}\]](http://latex.artofproblemsolving.com/5/e/b/5eb256119db8c13e088b441171647847540d63f4.png)
Alternate Solution
Extend two radii from the larger circle to the centers of the two smaller circles above (or below -- it's irrelevant). This forms a right triangle of sides 
. The length of the hypotenuse of the right triangle plus twice the radius of the smaller circle is equal to the side of the square. It follows, then ![\[A = (2+3\sqrt{2})^2 = 22 + 12\sqrt{2} \Rightarrow \text{(B)}\]](http://latex.artofproblemsolving.com/e/0/7/e07b0c88ba7b2e22e5ce17d506b71251b0674ed6.png)
See Also
| 2007 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Problem 16 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
