Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2021 MPFG Problem 19: Difference between revisions

← Older edit
Cassphe (talk | contribs)
editor
207 edits
Cassphe (talk | contribs)
editor
207 edits
 
Line 4: Line 4:


==Solution 1==
==Solution 1==
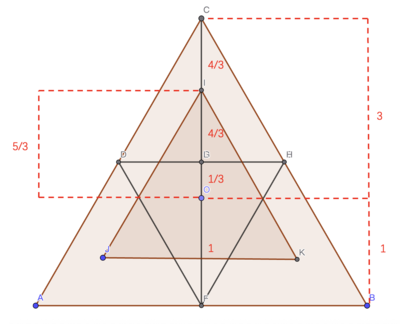
Connect <math>O</math> with the 4 vertices of <math>T</math>. Extend the line made by connecting the top vertex of <math>T</math> with <math>O</math>, intersecting at the base/vertex of <math>t</math>.  
Connect <imath>O</imath> with the 4 vertices of <imath>T</imath>. Extend the line made by connecting the top vertex of <imath>T</imath> with <imath>O</imath>, intersecting at the base/vertex of <imath>t</imath>.  


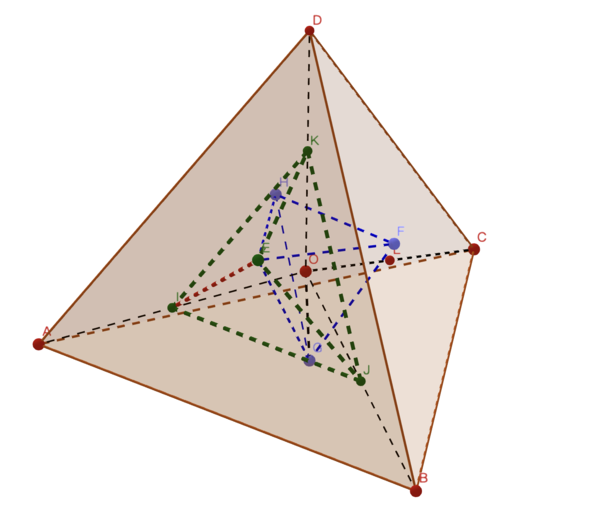
<math>S</math> equals to <math>1</math> regular tetrahedron with <math>4</math> protruding tetrahedrons.
<imath>S</imath> equals to <imath>1</imath> regular tetrahedron with <imath>4</imath> protruding tetrahedrons.


[[File:New3d.png|600px|center]]  
[[File:New3d.png|600px|center]]  
Line 12: Line 12:
[[File:2d.png|400px|]] [[File:Protrudes.png|500px|]]  
[[File:2d.png|400px|]] [[File:Protrudes.png|500px|]]  


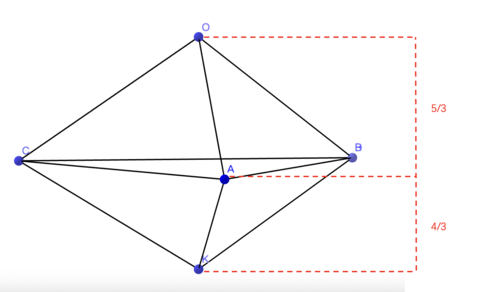
<math>S_{tetra} = (\frac{5}{3})^3 = \frac{125}{27}</math>
<imath>S_{tetra} = (\frac{5}{3})^3 = \frac{125}{27}</imath>


<math>S_{total} = \frac{125}{27} \cdot (1+\frac{\frac{4}{3}}{\frac{5}{3}}) = \boxed{\frac{25}{3}}</math>
<imath>S_{total} = \frac{125}{27} \cdot (1+\frac{\frac{4}{3}}{\frac{5}{3}}) = \boxed{\frac{25}{3}}</imath>


~cassphe
~cassphe

Latest revision as of 09:28, 7 November 2025

Problem

Let $T$ be a regular tetrahedron. Let $t$ be the regular tetrahedron whose vertices are the centers of the faces of $T$. Let $O$ be the circumcenter of either tetrahedron. Given a point $P$ different from $O$, let $m(P)$ be the midpoint of the points of intersection of the ray $\overrightarrow{OP}$ with $t$ and $T$. Let $S$ be the set of eight points m(P) where P is a vertex of either $t$ or $T$. What is the volume of the convex hull of $S$ divided by the volume of $t$? Express your answer as a fraction in simplest form.

Solution 1

Connect $O$ with the 4 vertices of $T$. Extend the line made by connecting the top vertex of $T$ with $O$, intersecting at the base/vertex of $t$.

$S$ equals to $1$ regular tetrahedron with $4$ protruding tetrahedrons.

$S_{tetra} = (\frac{5}{3})^3 = \frac{125}{27}$

$S_{total} = \frac{125}{27} \cdot (1+\frac{\frac{4}{3}}{\frac{5}{3}}) = \boxed{\frac{25}{3}}$

~cassphe

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2021_MPFG_Problem_19&oldid=266915"