2022 MPFG Problem19: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| Line 17: | Line 17: | ||
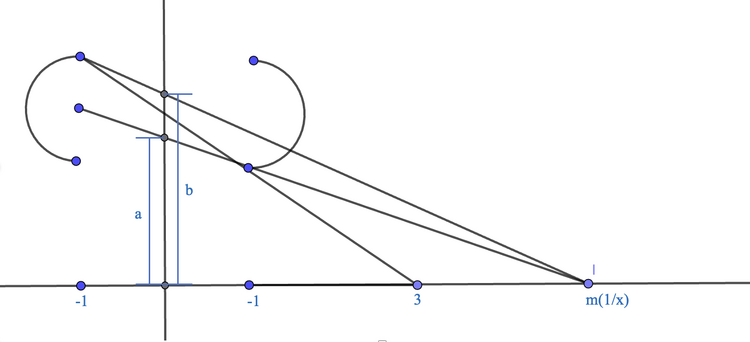
Let <imath>m=\frac{1}{x}</imath>. | Let <imath>m=\frac{1}{x}</imath>. | ||
[[File: | [[File:whynotworking.png|750px|center]] | ||
<imath>\frac{1}{a} = \frac{m-1}{m} ==> a=\frac{m}{m-1} = \frac{\frac{1}{x}}{\frac{1}{x}-1} = \frac{1}{1-x} = \frac{1}{y_1}</imath> | <imath>\frac{1}{a} = \frac{m-1}{m} ==> a=\frac{m}{m-1} = \frac{\frac{1}{x}}{\frac{1}{x}-1} = \frac{1}{1-x} = \frac{1}{y_1}</imath> | ||
Revision as of 08:47, 7 November 2025
Problem
Let ![]() be the semicircular arc defined by
be the semicircular arc defined by
![]() Let
Let ![]() be the semicircular arc defined by
be the semicircular arc defined by
![]()
Let ![]() be the locus of points
be the locus of points ![]() such that
such that ![]() is the intersection of two lines, one of the form
is the intersection of two lines, one of the form ![]() where
where ![]() and the other of the form
and the other of the form ![]() where
where ![]() . What is the area of
. What is the area of ![]() ? Express your answer as a fraction in simplest form.
? Express your answer as a fraction in simplest form.
Solution 1
Because ![]() is a solution set of
is a solution set of ![]() , which means that the
, which means that the ![]() coordinates are on the line of
coordinates are on the line of ![]() .
.
![]()
![]()
Let ![]() .
.
![]()
![]()
![]()
and m(![]() ) ranging from 3 to infinite
) ranging from 3 to infinite ![]()
![]() ,
, ![]()
![]() (times 2 because on both sides)
(times 2 because on both sides)

~cassphe









