Bisector: Difference between revisions
| Line 5: | Line 5: | ||
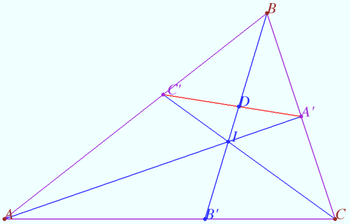
Let <math>AA', BB',</math> and <math>CC'</math> be the bisectors of <math>\triangle ABC.</math> | Let <math>AA', BB',</math> and <math>CC'</math> be the bisectors of <math>\triangle ABC.</math> | ||
he segments <math>BB'</math> and <math>A'C'</math> meet at point <math>D.</math> Find <cmath>\frac {BI}{BB'}, \frac { | he segments <math>BB'</math> and <math>A'C'</math> meet at point <math>D.</math> Find <cmath>\frac {BI}{BB'}, \frac {DA'}{DC'}, \frac {BD}{BB'}.</cmath> | ||
<i><b>Solution</b></i> | <i><b>Solution</b></i> | ||
Revision as of 16:12, 7 December 2023
Division of bisector
Let a triangle 
be given.
Let 
and 
be the bisectors of 
he segments 
and 
meet at point 
Find ![\[\frac {BI}{BB'}, \frac {DA'}{DC'}, \frac {BD}{BB'}.\]](http://latex.artofproblemsolving.com/5/1/4/514f96e06e7dd7f44797855eb8ce5f956663504a.png)
Solution
![\[\frac {BA'}{CA'} = \frac {BA}{CA} = \frac {c}{b}, BA' + CA' = BC = a \implies BA' = \frac {a \cdot c}{b+c}.\]](http://latex.artofproblemsolving.com/4/f/d/4fde431607d6e48344816a4f464a1e111879b731.png)
Similarly 
![\[\frac {BI}{IB'} = \frac {a}{B'C} = \frac{a+c}{b} \implies \frac {BI}{BB'} = \frac {a+c}{a + b +c}.\]](http://latex.artofproblemsolving.com/c/2/9/c29e89101ea63d35bfc04f787c84588fba11f410.png)
![\[\frac {DA'}{DC'} = \frac {BA'}{BC'} = \frac {a+ b}{b +c}.\]](http://latex.artofproblemsolving.com/a/a/4/aa4500b7d5b2f65f09c84e3455da66dccb16ca1d.png)
Denote 
Bisector 
Bisector 
![\[\frac {BD}{BB'} = \frac{a+c}{a+2b+c}.\]](http://latex.artofproblemsolving.com/3/4/e/34edec2d0145ed29a1b4137b26a852d12efdc5e3.png)
vladimir.shelomovskii@gmail.com, vvsss
