1997 AIME Problems/Problem 13: Difference between revisions
mNo edit summary |
non-rigorous trial-and-error. |
||
| Line 2: | Line 2: | ||
Let <math>S</math> be the set of points in the Cartesian plane that satisfy <center><math>\Big|\big||x|-2\big|-1\Big|+\Big|\big||y|-2\big|-1\Big|=1.</math></center> If a model of <math>S</math> were built from wire of negligible thickness, then the total length of wire required would be <math>a\sqrt{b}</math>, where <math>a</math> and <math>b</math> are positive integers and <math>b</math> is not divisible by the square of any prime number. Find <math>a+b</math>. | Let <math>S</math> be the set of points in the Cartesian plane that satisfy <center><math>\Big|\big||x|-2\big|-1\Big|+\Big|\big||y|-2\big|-1\Big|=1.</math></center> If a model of <math>S</math> were built from wire of negligible thickness, then the total length of wire required would be <math>a\sqrt{b}</math>, where <math>a</math> and <math>b</math> are positive integers and <math>b</math> is not divisible by the square of any prime number. Find <math>a+b</math>. | ||
__TOC__ | |||
== Solution == | == Solution == | ||
{{ | === Solution 1 === | ||
:''This solution is non-rigorous.'' | |||
Let <math>f(x) = \Big|\big||x|-2\big|-1\Big|</math>, <math>f(x) \ge 0</math>. Then <math>f(x) + f(y) = 1 \Longrightarrow f(x), f(y) \le 1 \Longrightarrow x, y \le 4</math>. We only have a <math>4\times 4</math> area, so guessing points and graphing won't be too bad of an idea. Since <math>f(x) = f(-x)</math>, there's a symmetry about all four [[quadrant]]s, so just consider the first quadrant. We now gather some points: | |||
{| class="wikitable" | |||
|- | |||
| <math>f(1) = 0</math> || <math>f(0.1) = 0.9</math> | |||
|- | |||
| <math>f(2) = 1</math> || <math>f(0.9) = 0.1</math> | |||
|- | |||
| <math>f(3) = 0</math> || <math>f(1.1) = 0.1</math> | |||
|- | |||
| <math>f(4) = 1</math> || <math>f(1.9) = 0.9</math> | |||
|- | |||
| <math>f(0.5) = 0.5</math> || <math>f(2.1) = 0.9</math> | |||
|- | |||
| <math>f(1.5) = 1.5</math> || <math>f(2.9) = 0.1</math> | |||
|- | |||
| <math>f(2.5) = 2.5</math> || <math>f(3.1) = 0.1</math> | |||
|- | |||
| <math>f(3.5) = 3.5</math> || <math>f(3.9) = 0.9</math> | |||
|} | |||
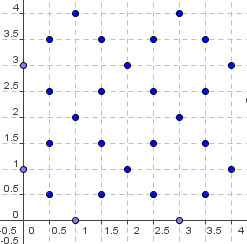
We can now graph the pairs of points which add up to <math>1</math>. Just using the first column of information gives us an interesting [[lattice]] pattern: | |||
[[Image:1997_AIME-13a.png]] | |||
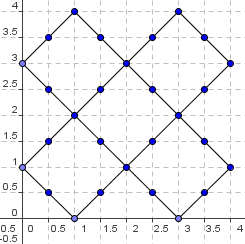
Plotting the remaining points and connecting lines, the graph looks like: | |||
[[Image:1997_AIME-13b.png]] | |||
Calculating the lengths is now easy; each rectangle has sides of <math>\sqrt{2}, 3\sqrt{2}</math>, so the answer is <math>4(\sqrt{2} + 3\sqrt{2}) = 16\sqrt{2}</math>. For all four quadrants, this is <math>64\sqrt{2}</math>, and <math>a+b=\boxed{066}</math>. | |||
=== Solution 2 === | |||
== See also == | == See also == | ||
{{AIME box|year=1997|num-b=12|num-a=14}} | {{AIME box|year=1997|num-b=12|num-a=14}} | ||
[[Category:Intermediate Algebra Problems]] | |||
Revision as of 21:10, 23 November 2007
Problem
Let 
be the set of points in the Cartesian plane that satisfy
If a model of were built from wire of negligible thickness, then the total length of wire required would be 
, where 
and 
are positive integers and is not divisible by the square of any prime number. Find 
.
Solution
Solution 1
- This solution is non-rigorous.
Let 
, 
. Then 
. We only have a 
area, so guessing points and graphing won't be too bad of an idea. Since 
, there's a symmetry about all four quadrants, so just consider the first quadrant. We now gather some points:
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
 |
|
We can now graph the pairs of points which add up to 
. Just using the first column of information gives us an interesting lattice pattern:
Plotting the remaining points and connecting lines, the graph looks like:
Calculating the lengths is now easy; each rectangle has sides of 
, so the answer is 
. For all four quadrants, this is 
, and 
.
Solution 2
See also
| 1997 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
