Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

1994 AHSME Problems/Problem 28: Difference between revisions

← Older editNewer edit →
Isabelchen (talk | contribs)
editor
1,109 edits
No edit summary
Line 3: Line 3:


<math> \textbf{(A)}\ 0 \qquad\textbf{(B)}\ 1 \qquad\textbf{(C)}\ 2 \qquad\textbf{(D)}\ 3 \qquad\textbf{(E)}\ 4</math>
<math> \textbf{(A)}\ 0 \qquad\textbf{(B)}\ 1 \qquad\textbf{(C)}\ 2 \qquad\textbf{(D)}\ 3 \qquad\textbf{(E)}\ 4</math>
==Solution==
 
==Solution 1==


The line with <math>x</math>-intercept  <math>a</math> and <math>y</math>-intercept <math>b</math> is given by the equation <math>\frac{x}{a} + \frac{y}{b} = 1</math>.  We are told <math>(4,3)</math> is on the line so  
The line with <math>x</math>-intercept  <math>a</math> and <math>y</math>-intercept <math>b</math> is given by the equation <math>\frac{x}{a} + \frac{y}{b} = 1</math>.  We are told <math>(4,3)</math> is on the line so  
Line 10: Line 11:


Since <math>a</math> and <math>b</math> are integers, this equation holds only if <math>(a-4)</math> is a factor of <math>12</math>.  The factors are <math>1, 2, 3, 4, 6, 12</math> which means <math>a</math> must be one of <math>5, 6, 7, 8, 10, 16</math>.  The only members of this list which are prime are <math>a=5</math> and <math>a=7</math>, so the number of solutions is <math>\boxed{\textbf{(C) } 2}</math>.
Since <math>a</math> and <math>b</math> are integers, this equation holds only if <math>(a-4)</math> is a factor of <math>12</math>.  The factors are <math>1, 2, 3, 4, 6, 12</math> which means <math>a</math> must be one of <math>5, 6, 7, 8, 10, 16</math>.  The only members of this list which are prime are <math>a=5</math> and <math>a=7</math>, so the number of solutions is <math>\boxed{\textbf{(C) } 2}</math>.
==Solution 2==
[[File:1984AHSMEP28.png|500px|center]]
Let <math>C = (4,3)</math>, <math>DF=a</math>, and <math>AD=b</math>. As stated in the problem, the <math>x</math>-intercept <math>DF=a</math> is a positive prime number, and the <math>y</math>-intercept <math>AD=b</math> is a positive integer.
Through similar triangles, <math>\frac{AB}{BC}=\frac{CE}{EF}</math>, <math>\frac{b-3}{4}=\frac{3}{a-4}</math>, <math>(a-4)(b-3)=12</math>
The only cases where <math>a</math> is:
<math>\begin{cases}
a-4=1 & a=5 \\
b-3=12 & b=15
\end{cases}<cmath>
and
</cmath>\begin{cases}
a-4=3 & a=7 \\
b-3=4 & b=5
\end{cases}</math><math>
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
In the </math>xy<math>-plane, how many lines whose </math>x<math>-intercept is a positive prime number and whose </math>y<math>-intercept is a positive integer pass through the point </math>(4,3)$?


==See Also==
==See Also==

Revision as of 06:55, 28 September 2023

Problem

In the $xy$-plane, how many lines whose $x$-intercept is a positive prime number and whose $y$-intercept is a positive integer pass through the point $(4,3)$?

$\textbf{(A)}\ 0 \qquad\textbf{(B)}\ 1 \qquad\textbf{(C)}\ 2 \qquad\textbf{(D)}\ 3 \qquad\textbf{(E)}\ 4$

Solution 1

The line with $x$-intercept $a$ and $y$-intercept $b$ is given by the equation $\frac{x}{a} + \frac{y}{b} = 1$. We are told $(4,3)$ is on the line so

\[\frac{4}{a} + \frac{3}{b} = 1 \implies ab - 4b - 3a = 0 \implies (a-4)(b-3)=12\]

Since $a$ and $b$ are integers, this equation holds only if $(a-4)$ is a factor of $12$. The factors are $1, 2, 3, 4, 6, 12$ which means $a$ must be one of $5, 6, 7, 8, 10, 16$. The only members of this list which are prime are $a=5$ and $a=7$, so the number of solutions is $\boxed{\textbf{(C) } 2}$.

Solution 2

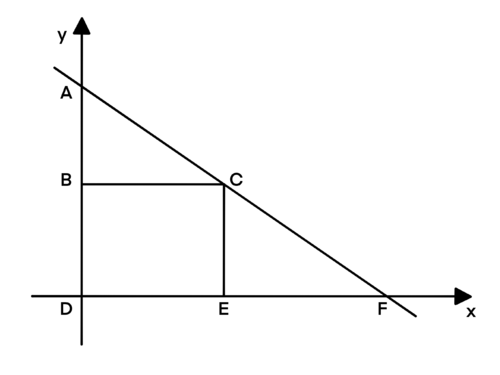
Let $C = (4,3)$, $DF=a$, and $AD=b$. As stated in the problem, the $x$-intercept $DF=a$ is a positive prime number, and the $y$-intercept $AD=b$ is a positive integer.

Through similar triangles, $\frac{AB}{BC}=\frac{CE}{EF}$, $\frac{b-3}{4}=\frac{3}{a-4}$, $(a-4)(b-3)=12$

The only cases where $a$ is: $\begin{cases} a-4=1 & a=5 \\ b-3=12 & b=15 \end{cases}<cmath>

and

</cmath>\begin{cases} a-4=3 & a=7 \\ b-3=4 & b=5 \end{cases}$ (Error compiling LaTeX. Unknown error_msg)$~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]

In the$ (Error compiling LaTeX. Unknown error_msg)xy$-plane, how many lines whose$x$-intercept is a positive prime number and whose$y$-intercept is a positive integer pass through the point$(4,3)$?

See Also

1994 AHSME (Problems • Answer Key • Resources)
Preceded by
Problem 27 		Followed by
Problem 29
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30
All AHSME Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America.

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=1994_AHSME_Problems/Problem_28&oldid=198700"