Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Gauss line: Difference between revisions

Vvsss (talk | contribs)
editor
2,736 edits
Created page with "The Gauss line (or Gauss–Newton line) is the line joining the midpoints of the three diagonals of a complete quadrilateral. ==Existence of the Gauss line== The complete qu..."
 
Vvsss (talk | contribs)
editor
2,736 edits
 
Line 2: Line 2:


==Existence of the Gauss line==
==Existence of the Gauss line==
The complete quadilateral <math>ABCDEF (E = AD \cap BC, F = AB \cap CD)</math> be given.
[[File:Gauss line 1.png|400px|right]]
Denote <math>O</math> the midpoint <math>AC, O_1</math> the midpoint <math>BD, O_2</math> the midpoint <math>EF, H</math> the orthocenter of <math>\triangle CDE, H_1</math> the orthocenter of <math>\triangle BCF, H_2</math> the orthocenter of <math>\triangle ABE, H_3</math> the orthocenter of <math>\triangle ADF, \omega</math> the circle with diameter <math>AC, \Omega</math> the circle with diameter <math>BD, \theta</math> the circle with diameter <math>EF, \alpha</math> the circle with diameter <math>CD, \beta</math> the circle with diameter <math>CE.</math>
The complete quadilateral <math>ABCDEF</math> <math>(E = AD \cap BC, F = AB \cap CD)</math> be given.
Denote <math>O, O_1, O_2</math> the midpoints of <math>AC, BD, EF,</math> respectively.


Prove
Denote <math>H, H_1, H_2, H_3</math> the orthocenters of the <math>\triangle CDE, \triangle BCF, \triangle ABE, \triangle ADF,</math> respectively.


a)  points <math>O, O_1, O_2</math> are collinear;
Denote <math>\omega, \Omega,  \theta, \alpha,</math> and <math>\beta</math> the circles with diameters <math>AC, BD, EF, CD,</math> and <math>CE,</math> respectively.
 
Prove a)  points <math>O, O_1, O_2</math> are collinear;


b) <math>OO_1 \perp HH_1;</math>
b) <math>OO_1 \perp HH_1;</math>
 
c) points <math>H, H_1, H_2, H_3</math> are collinear.
c) points <math>H, H_1, H_2, H_3</math> are collinear.


<i><b>Proof</b></i>
<i><b>Proof</b></i>


Let <cmath>C_1 \in AD, CC_1 \perp DE, D_1 \in BC, DD_1 \perp CE, E_1 \in CD, EE_1 \perp CD \implies</cmath>
Let <cmath>C_1 \in AD, CC_1 \perp AD, D_1 \in BC, DD_1 \perp BC, E_1 \in CD, EE_1 \perp CD \implies</cmath>
<cmath>H = CC_1 \cap DD_1 \cap EE_1, C_1 \in \alpha, D_1 \in \alpha, C_1 \in \beta, E_1 \in \alpha, \implies</cmath>
<cmath>H = CC_1 \cap DD_1 \cap EE_1, C_1 \in \alpha, D_1 \in \alpha, C_1 \in \beta, E_1 \in \beta \implies</cmath>
<math>H</math> is the radical center of <math>\omega, \Omega,</math> and <math>\alpha \implies H</math> lies on the radical axes of <math>\omega</math> and <math>\Omega.</math>
<math>H</math> is the radical center of <math>\omega, \Omega,</math> and <math>\alpha \implies H</math> lies on the radical axes of <math>\omega</math> and <math>\Omega.</math>


Line 23: Line 26:
Similarly, using circles with diameters <math>BC</math> and <math>FC</math> one can prove that <math>H_1</math> lies on the radical axes of <math>\omega</math> and <math>\Omega</math> and on the radical axes of <math>\omega</math> and <math>\theta.</math>
Similarly, using circles with diameters <math>BC</math> and <math>FC</math> one can prove that <math>H_1</math> lies on the radical axes of <math>\omega</math> and <math>\Omega</math> and on the radical axes of <math>\omega</math> and <math>\theta.</math>


Therefore <math>HH_1 \perp OO_1, HH_1 \perp OO_2 \implies</math> points <math>O, O_1,</math> and <math>O_2</math> are collinear and <math>HH_1</math> is the perpendicular to the line <math>OO_1O_2.</math>.
Therefore <math>HH_1 \perp OO_1, HH_1 \perp OO_2 \implies</math> points <math>O, O_1,</math> and <math>O_2</math> are collinear.
Similarly,  one can prove that <math>H_2</math> and <math>H_3</math> lie on the radical axes of <math>\omega</math> and <math>\Omega \implies </math>  points H, H_1, H_2$ and H_3 are collinear.
 
It is clear that <math>HH_1</math> is the perpendicular to the line <math>OO_1O_2.</math>.
 
Similarly,  one can prove that <math>H_2</math> and <math>H_3</math> lie on the radical axes of <math>\omega</math> and <math>\Omega \implies </math>  points <math>H, H_1, H_2</math> and <math>H_3</math> are collinear.
*[[Steiner line]]
'''vladimir.shelomovskii@gmail.com, vvsss'''

Latest revision as of 05:35, 26 April 2023

The Gauss line (or Gauss–Newton line) is the line joining the midpoints of the three diagonals of a complete quadrilateral.

Existence of the Gauss line

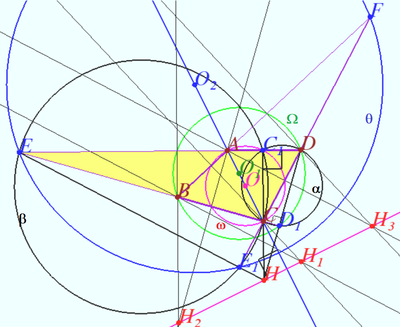
The complete quadilateral $ABCDEF$ $(E = AD \cap BC, F = AB \cap CD)$ be given. Denote $O, O_1, O_2$ the midpoints of $AC, BD, EF,$ respectively.

Denote $H, H_1, H_2, H_3$ the orthocenters of the $\triangle CDE, \triangle BCF, \triangle ABE, \triangle ADF,$ respectively.

Denote $\omega, \Omega, \theta, \alpha,$ and $\beta$ the circles with diameters $AC, BD, EF, CD,$ and $CE,$ respectively.

Prove a) points $O, O_1, O_2$ are collinear;

b) $OO_1 \perp HH_1;$

c) points $H, H_1, H_2, H_3$ are collinear.

Proof

Let \[C_1 \in AD, CC_1 \perp AD, D_1 \in BC, DD_1 \perp BC, E_1 \in CD, EE_1 \perp CD \implies\] \[H = CC_1 \cap DD_1 \cap EE_1, C_1 \in \alpha, D_1 \in \alpha, C_1 \in \beta, E_1 \in \beta \implies\] $H$ is the radical center of $\omega, \Omega,$ and $\alpha \implies H$ lies on the radical axes of $\omega$ and $\Omega.$

$H$ is the radical center of $\omega, \theta,$ and $\beta \implies H$ lies on the radical axes of $\omega$ and $\theta.$

Similarly, using circles with diameters $BC$ and $FC$ one can prove that $H_1$ lies on the radical axes of $\omega$ and $\Omega$ and on the radical axes of $\omega$ and $\theta.$

Therefore $HH_1 \perp OO_1, HH_1 \perp OO_2 \implies$ points $O, O_1,$ and $O_2$ are collinear.

It is clear that $HH_1$ is the perpendicular to the line $OO_1O_2.$.

Similarly, one can prove that $H_2$ and $H_3$ lie on the radical axes of $\omega$ and $\Omega \implies$ points $H, H_1, H_2$ and $H_3$ are collinear.

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=Gauss_line&oldid=192518"