1991 AIME Problems/Problem 4: Difference between revisions
m →See also: typo |
mNo edit summary |
||
| Line 3: | Line 3: | ||
== Solution == | == Solution == | ||
<center>[[Image:AIME_1991_Solution_04.png]]</center> | |||
The [[range]] of the [[sine]] function is <math>-1 \le y \le 1</math>. It is [[periodic function|periodic]] (in this problem) with a period of <math>\frac{2}{5}</math>. | The [[range]] of the [[sine]] function is <math>-1 \le y \le 1</math>. It is [[periodic function|periodic]] (in this problem) with a period of <math>\frac{2}{5}</math>. | ||
| Line 10: | Line 10: | ||
== See also == | == See also == | ||
*[[Trigonometry]] | *[[Trigonometry]] | ||
*[http://www.artofproblemsolving.com/Forum/viewtopic.php?t=70180 Aops Topic] | |||
{{AIME box|year=1991|num-b=3|num-a=5}} | {{AIME box|year=1991|num-b=3|num-a=5}} | ||
[[Category:Intermediate Algebra Problems]] | [[Category:Intermediate Algebra Problems]] | ||
Revision as of 18:40, 3 November 2007
Problem
How many real numbers 
satisfy the equation 
?
Solution
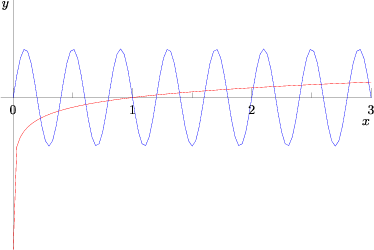
The range of the sine function is 
. It is periodic (in this problem) with a period of 
.
Thus, 
, and 
. The solutions for 
occur in the domain of 
. When 
the logarithm function returns a positive value; up to 
it will pass through the sine curve. There are exactly 10 intersections of five periods (every two integral values of ) of the sine curve and another curve that is 
, so there are 
values (the subtraction of 6 since all the “intersections” when 
must be disregarded). When 
, there is exactly 
touching point between the two functions: 
. When 
or , we can count 
more solutions. The solution is 
.
See also
| 1991 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
