2004 AIME I Problems/Problem 10: Difference between revisions
I_like_pie (talk | contribs) No edit summary |
should have a solution soon |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
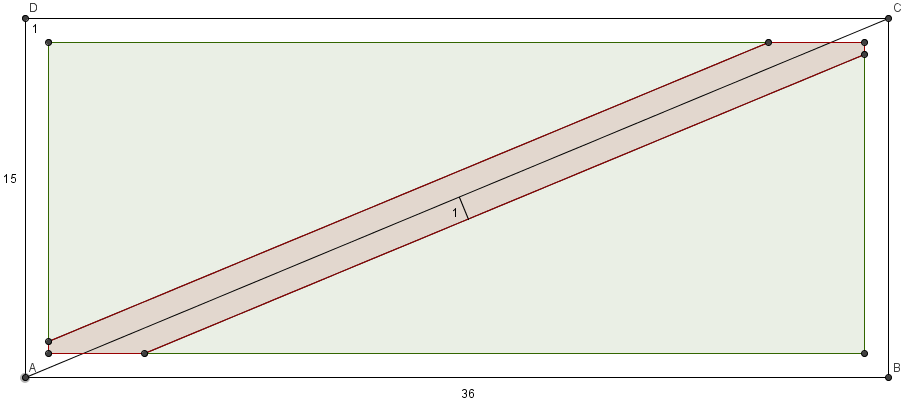
A circle of radius 1 is randomly placed in a 15-by-36 rectangle <math> ABCD </math> so that the circle lies completely within the rectangle. Given that the | A [[circle]] of [[radius]] 1 is randomly placed in a 15-by-36 [[rectangle]] <math> ABCD </math> so that the circle lies completely within the rectangle. Given that the p[[robability]] that the circle will not touch diagonal <math> AC </math> is <math> m/n, </math> where <math> m </math> and <math> n </math> are relatively prime positive integers. Find <math> m + n. </math> | ||
== Solution == | == Solution == | ||
[[Image:2004_I_AIME-10.png]] | |||
== See also == | == See also == | ||
{{AIME box|year=2004|num-b=9|num-a=11}} | |||
[[Category:Intermediate Geometry Problems]] | |||
Revision as of 18:30, 13 October 2007
Problem
A circle of radius 1 is randomly placed in a 15-by-36 rectangle 
so that the circle lies completely within the rectangle. Given that the probability that the circle will not touch diagonal 
is 
where 
and 
are relatively prime positive integers. Find 
Solution
See also
| 2004 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
