2020 USAMO Problems/Problem 1: Difference between revisions
| Line 19: | Line 19: | ||
The area of <math>\triangle OO_1O_2</math> is minimized if <math>CX \perp AB</math> because | The area of <math>\triangle OO_1O_2</math> is minimized if <math>CX \perp AB</math> because | ||
<cmath>\frac {[OO_1O_2]} {[ABC]} = \left(\frac {O_1 O_2} {AB}\right)^2 \ge \left(\frac {EF} {AB}\right)^2 = \frac {1}{4}.</cmath> | <cmath>\frac {[OO_1O_2]} {[ABC]} = \left(\frac {O_1 O_2} {AB}\right)^2 \ge \left(\frac {EF} {AB}\right)^2 = \frac {1}{4}.</cmath> | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | |||
==Video Solution== | ==Video Solution== | ||
https://www.youtube.com/watch?v=m157cfw0vdE | https://www.youtube.com/watch?v=m157cfw0vdE | ||
Revision as of 10:49, 16 September 2022
Problem 1
Let 
be a fixed acute triangle inscribed in a circle 
with center 
. A variable point 
is chosen on minor arc 
of , and segments 
and meet at 
. Denote by 
and 
the circumcenters of triangles 
and 
, respectively. Determine all points for which the area of triangle 
is minimized.
Solution
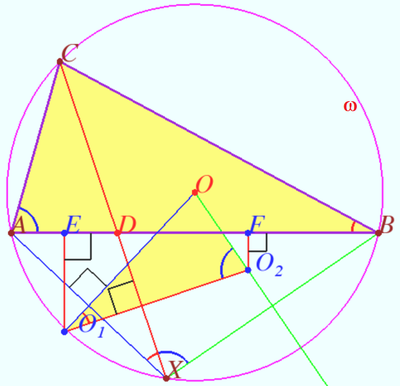
Let 
be midpoint 
Let 
be midpoint 
![\[EF = ED + FD = \frac {AD}{2} + \frac {BD}{2} = \frac {AB}{2}.\]](http://latex.artofproblemsolving.com/6/a/3/6a3d1a035769408e01b3d7c52555ad01d17da147.png)
and are the bases of perpendiculars dropped from and 
respectively.
Therefore 
![\[CX \perp O_1O_2, AX \perp O_1O \implies \angle O O_1O_2 = \angle AXC\]](http://latex.artofproblemsolving.com/2/d/b/2db8e3f3cb6a7c5558f0082c93abfc8a85441758.png)
is cyclic) 
Similarly 
The area of 
is minimized if 
because
![\[\frac {[OO_1O_2]} {[ABC]} = \left(\frac {O_1 O_2} {AB}\right)^2 \ge \left(\frac {EF} {AB}\right)^2 = \frac {1}{4}.\]](http://latex.artofproblemsolving.com/2/3/2/23291b4af828ea47539e00ea3817a4659a7add9e.png)
vladimir.shelomovskii@gmail.com, vvsss
