2005 AMC 10A Problems/Problem 23: Difference between revisions

Revision as of 05:51, 16 July 2022

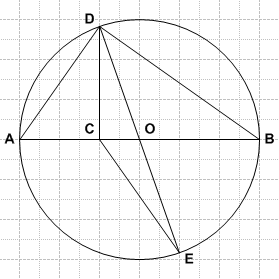
Problem

Let $AB$ be a diameter of a circle and let $C$ be a point on $AB$ with $2\cdot AC=BC$ . Let $D$ and $E$ be points on the circle such that $DC \perp AB$ and $DE$ is a second diameter. What is the ratio of the area of $\triangle DCE$ to the area of $\triangle ABD$ ?

$[asy] unitsize(2.5cm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=3; pair O=(0,0), C=(-1/3.0), B=(1,0), A=(-1,0); pair D=dir(aCos(C.x)), E=(-D.x,-D.y); draw(A--B--D--cycle); draw(D--E--C); draw(unitcircle,white); drawline(D,C); dot(O); clip(unitcircle); draw(unitcircle); label("$E$",E,SSE); label("$B$",B,E); label("$A$",A,W); label("$D$",D,NNW); label("$C$",C,SW); draw(rightanglemark(D,C,B,2));[/asy]$

$\textbf{(A) } \frac{1}{6}\qquad \textbf{(B) } \frac{1}{4}\qquad \textbf{(C) } \frac{1}{3}\qquad \textbf{(D) } \frac{1}{2}\qquad \textbf{(E) } \frac{2}{3}$

Solution 1

WLOG, Let us assume that the diameter is of length $1$ .

The length of $AC$ is $\frac{1}{3}$ and $CO$ is $\frac{1}{2}-\frac{1}{3} = \frac{1}{6}$ .

$OD$ is the radius of the circle, which is $\frac{1}{2}$ , so using the Pythagorean Theorem the height $CD$ of $\triangle DCO$ is $\sqrt{\left(\frac{1}{2}\right)^2-\left(\frac{1}{6}\right)^2} = \frac{\sqrt{2}}{3}$ . This is also the height of the $\triangle ABD$ .

The area of $\triangle DCO$ is $\frac{1}{2}\cdot\frac{1}{6}\cdot\frac{\sqrt{2}}{3}$ = $\frac{\sqrt{2}}{36}$ .

The height of $\triangle DCE$ can be found using the area of $\triangle DCO$ and $DO$ as base.

Hence, the height of $\triangle DCE$ is $\dfrac{\dfrac{\sqrt{2}}{36}}{\dfrac{1}{2}\cdot\dfrac{1}{2}}$ = $\dfrac{\sqrt{2}}{9}$ .

The diameter is the base for both the triangles $\triangle DCE$ and $\triangle ABD$ ,

Hence, the ratio of the area of $\triangle DCE$ to the area of $\triangle ABD$ is $\dfrac{\dfrac{\sqrt{2}}{9}}{\dfrac{\sqrt{2}}{3}}$ = $\boxed{\textbf{(C) }\frac{1}{3}}$

Solution 2

Since $\triangle DCE$ and $\triangle ABD$ share a base, the ratio of their areas is the ratio of their altitudes. Draw the altitude from $C$ to $DE$ .

$[asy] import graph; import olympiad; pair O,A,B,C,D,E,F; O=(0,0);A=(15,0);B=(-15,0);C=(5,0);D=(5,14.142135623730950488016887242097);E=(-5,-14.142135623730950488016887242097);F=(0.5555555555555555,1.5713484026367722764463208046774); draw(Circle((0,0),15)); draw(A--B);draw(D--E);draw(C--D);draw(C--E);draw(C--F);draw(A--D);draw(D--B); label("A",A,NE);label("B",B,W);label("C",C,SE);label("D",D,NE);label("E",E,SW);label("O",O,SW);label("F",F,NW); markscalefactor=0.2; draw(anglemark(C,F,D),blue);draw(anglemark(D,C,B),blue); [/asy]$ $OD=r, OC=\frac{1}{3}r$ .

Since $m\angle DCO=m\angle DFC=90^\circ$ , then $\triangle DCO\cong \triangle DFC$ . So the ratio of the two altitudes is $\frac{CF}{DC}=\frac{OC}{DO}=\boxed{\textbf{(C) }\frac{1}{3}}$

Solution 3

Say the center of the circle is point $O$ ; Without loss of generality, assume $AC=2$ , so $CB=4$ and the diameter and radius are $6$ and $3$ , respectively. Therefore, $CO=1$ , and $DO=3$ . The area of $\triangle DCE$ can be expressed as $\frac{1}{2}(CD)(6)\text{sin }(CDE).$ $\frac{1}{2}(CD)(6)$ happens to be the area of $\triangle ABD$ . Furthermore, $\text{sin } CDE = \frac{CO}{DO},$ or $\frac{1}{3}.$ Therefore, the ratio is $\boxed{\textbf{(C) }\frac{1}{3}}.$

Solution 5

$[asy] unitsize(2.5cm); defaultpen(fontsize(10pt)+linewidth(.8pt)); dotfactor=3; pair O=(0,0), C=(-1/3.0), B=(1,0), A=(-1,0); pair D=dir(aCos(C.x)), E=(-D.x,-D.y); draw(A--B--D--cycle); draw(D--E--C); draw(unitcircle,white); drawline(D,C); dot(O); clip(unitcircle); draw(unitcircle); label("$E$",E,SSE); label("$B$",B,E); label("$A$",A,W); label("$D$",D,NNW); label("$C$",C,SW); draw(rightanglemark(D,C,B,2)); [/asy]$

Let the point G be the reflection of point $D$ across $\overline{AB}$ . (Point G is on the circle).

Let $AC=x$ , then $BC=2x$ . The diameter is $3x$ . To find $DC$ , there are two ways (presented here):

1. Since $\overline{AB}$ is the diameter, $CD=CG$ . Using power of points, $AC\cdot BC=x\cdot2x=2x^{2}=CD^{2} \longrightarrow CD=x\sqrt{2}$ 2. Use the geometric mean theorem, $AC\cdot BC=x\cdot2x=2x^{2}=CD^{2} \longrightarrow CD=x\sqrt{2}$ (These are the same equations but obtained through different formulae)

Therefore $DG=2x\sqrt{2}$ . Since $\overline{DE}$ is a diameter, $\triangle DGE$ is right. By the Pythagorean theorem, $DE^{2}=GD^{2}+GE^{2} \longrightarrow \left(3x\right)^{2}=\left(2x\sqrt{2}\right)^{2}+GE^{2}$ $9x^{2}=8x^{2}+GE^{2} \longrightarrow GE^{2}=x^{2} \longrightarrow GE=x$

As established before, $\angle DGE$ is right (if you are unsure, look up "inscribed angle theorem", this is a special case of the theorem where the central angle measures $180^{\circ}$ ) so $GE=x$ is the altitude of $\triangle DCE$ , and $DC=x\sqrt{2}$ is the base. Therefore $\left[DCE\right]=\frac{1}{2}\cdot DC\cdot GE=\frac{1}{2}\cdot x\sqrt{2}\cdot x=\frac{x^{2}\sqrt{2}}{2}$

$AB=3x$ is the base of $\triangle ABD$ and $CD=x\sqrt{2}$ is the height. $\left[ABD\right]=\frac{1}{2}\cdot3x\cdot x\sqrt{2}=\frac{3x^{2}\sqrt{2}}{2}$

The required ratio is $\frac{\left[DCE\right]}{\left[ABD\right]}=\frac{\frac{x^{2}\sqrt{2}}{2}}{\frac{3x^{2}\sqrt{2}}{2}}=\frac{x^{2}\sqrt{2}}{2}\cdot\frac{2}{3x^{2}\sqrt{2}}=\frac{x^{2}\sqrt{2}}{3x^{2}\sqrt{2}}=\frac{1}{3}$ The answer is $\boxed{\textbf{(C) } \frac{1}{3}}$ .

~JH. L

Solution 5 (Video)

Video solution: https://youtu.be/i6eooSSJF64

2005 AMC 10A (Problems • Answer Key • Resources)
Preceded by Problem 22	Followed by Problem 24
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

Page

Toolbox

Search