Angle bisector: Difference between revisions
No edit summary |
|||
| Line 5: | Line 5: | ||
== Features of Angle Bisectors == | == Features of Angle Bisectors == | ||
In a triangle, the angle bisectors (which are [[cevian|cevians]]) will intersect at the [[incenter]] of the triangle. | [[Image:Incenter.PNG|left|thumb|300px|Triangle ''ABC'' with incenter ''I'', with angle bisectors (red), incircle (blue), and incenter (green)]] | ||
In a triangle, the angle bisectors (which are [[cevian|cevians]]) will all intersect at the [[incenter]] of the triangle. | |||
==See also== | ==See also== | ||
Revision as of 19:15, 15 September 2007
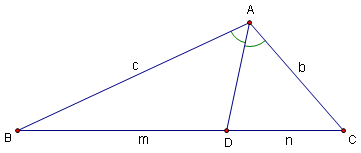
For an angle 
, the angle bisector of is the line from B such that the angle between this line and 
is equal to the angle between this line and 
.
Features of Angle Bisectors
In a triangle, the angle bisectors (which are cevians) will all intersect at the incenter of the triangle.
See also
This article is a stub. Help us out by expanding it.
