2021 JMPSC Sprint Problems/Problem 16: Difference between revisions
Mathdreams (talk | contribs) |
|||
| Line 6: | Line 6: | ||
==Solution== | ==Solution== | ||
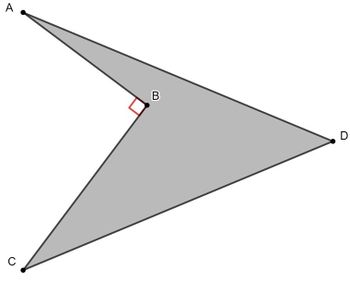
Notice that <math>[ABCD] = [ADC] - [ABC]</math> and <math>AC = \sqrt{12^2 + 16^2} = 20</math> by the Pythagorean Thereom. We then have that the area of triangle of <math>ADC</math> is <math>\frac{20 \cdot \sqrt{26^2 - 10^2}}{2} = 240</math>, and the area of triangle <math>ABC</math> is <math>\frac{12 \cdot 16}{2} = 96</math>, so the area of quadrilateral <math>ABCD</math> is <math>240 - 96 = 144</math>. | |||
~Mathdreams | |||