1991 AIME Problems/Problem 11: Difference between revisions
No edit summary |
mNo edit summary |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
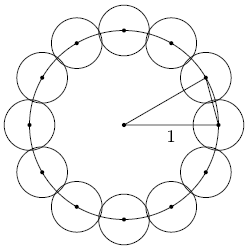
Twelve congruent disks are placed on a circle <math>C^{}_{}</math> of radius 1 in such a way that the twelve disks cover <math>C^{}_{}</math>, no two of the disks overlap, and so that each of the twelve disks is tangent to its two neighbors. The resulting arrangement of disks is shown in the figure below. The sum of the areas of the twelve disks can be written in the from <math>\pi(a-b\sqrt{c})</math>, where <math>a,b,c^{}_{}</math> are positive integers and <math>c^{}_{}</math> is not divisible by the square of any prime. Find <math>a+b+c^{}_{}</math>. | |||
[[Image:AIME_1991_Problem_11.gif]] | |||
== Solution == | == Solution == | ||
{{solution}} | |||
== See also == | == See also == | ||
{{AIME box|year=1991|num-b=10|num-a=12}} | |||
Revision as of 01:36, 2 March 2007
Problem
Twelve congruent disks are placed on a circle 
of radius 1 in such a way that the twelve disks cover , no two of the disks overlap, and so that each of the twelve disks is tangent to its two neighbors. The resulting arrangement of disks is shown in the figure below. The sum of the areas of the twelve disks can be written in the from 
, where 
are positive integers and 
is not divisible by the square of any prime. Find 
.
Solution
This problem needs a solution. If you have a solution for it, please help us out by adding it.
See also
| 1991 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
