Cyclic quadrilateral: Difference between revisions
| Line 7: | Line 7: | ||
In cyclic quadrilateral <math>ABCD</math>: | In cyclic quadrilateral <math>ABCD</math>: | ||
* <math>\angle A + \angle C = \angle B + \angle D = {180}^{o}</math> | * <math>\angle A + \angle C = \angle B + \angle D = {180}^{o} (Proven by drawing arcs connecting AC)</math> | ||
* <math>\angle ABD = \angle ACD</math> | * <math>\angle ABD = \angle ACD</math> | ||
* <math>\angle BCA = \angle BDA</math> | * <math>\angle BCA = \angle BDA</math> | ||
Revision as of 15:52, 31 May 2021
A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle. They have a number of interesting properties.
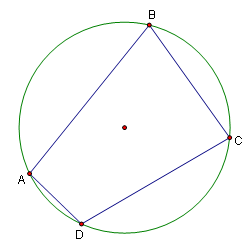
Properties
In cyclic quadrilateral ![]() :
:
Applicable Theorems/Formulae
The following theorems and formulae apply to cyclic quadrilaterals:
This article is a stub. Help us out by expanding it.









