Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2006 AIME I Problems/Problem 7: Difference between revisions

← Older editNewer edit →
Added a solution
Jbala (talk | contribs)
1,029 edits
No edit summary
Line 1: Line 1:
== Problem ==
== Problem ==
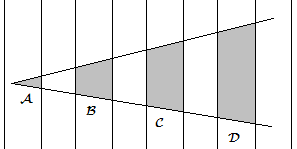
An [[angle]] is drawn on a set of equally spaced [[parallel]] [[line]]s as shown. The [[ratio]] of the [[area]] of shaded [[region]] <math> \mathcal{C} </math> to the area of shaded region <math> \mathcal{B} </math> is 11/5. Find the ratio of shaded region <math> \mathcal{D} </math> to the area of shaded region <math> \mathcal{A}.  </math>
An [[angle]] is drawn on a set of equally spaced [[parallel]] [[line]]s as shown. The [[ratio]] of the [[area]] of shaded [[region]] <math>C</math> to the area of shaded region <math>B</math> is 11/5. Find the ratio of shaded region <math>D</math> to the area of shaded region <math>A</math>.


[[Image:2006AimeA7.PNG]]
[[Image:2006AimeA7.PNG]]
Line 12: Line 12:
Since the area of the triangle is equal to <math>\frac{1}{2}bh</math>,
Since the area of the triangle is equal to <math>\frac{1}{2}bh</math>,


<cmath>
Region <math>C</math>/Region <math>B</math>  = \frac{11}{5}
\frac{\textrm{Region\ }\mathcal{C}}{\textrm{Region\ }\mathcal{B}} = \frac{11}{5}
= \frac{\frac 12(5-s)^2 - \frac 12(4-s)^2}{\frac 12(3-s)^2 - \frac12(2-s)^2}
= \frac{\frac 12(5-s)^2 - \frac 12(4-s)^2}{\frac 12(3-s)^2 - \frac12(2-s)^2}
</cmath>
<math></math>


Solve this to find that <math>s = \frac{5}{6}</math>.
Solve this to find that <math>s = \frac{5}{6}</math>.


Using the same reasoning as above, we get <math>\frac{\textrm{Region\ }\mathcal{D}}{\textrm{Region\ }\mathcal{A}} = \frac{\frac 12(7-s)^2 - \frac 12(6-s)^2}{\frac 12(1-s)^2}</math>, which is <math>\boxed{408}</math>.
Using the same reasoning as above, we get Region <math>D</math>/Region <math>A</math> = \frac{\frac 12(7-s)^2 - \frac 12(6-s)^2}{\frac 12(1-s)^2}<math>, which is </math>\boxed{408}<math>.


== Solution 2 ==
== Solution 2 ==


Note that the sections between the two transversals can be divided into one small triangle and a number of trapezoids. Let one side length (not on a parallel line) of the small triangle be <math>x</math> and the area of it be <math>x^2</math>. Also, let all sections of the line on the same side as the side with length <math>x</math> on a trapezoid be equal to <math>1</math>.  
Note that the sections between the two transversals can be divided into one small triangle and a number of trapezoids. Let one side length (not on a parallel line) of the small triangle be </math>x<math> and the area of it be </math>x^2<math>. Also, let all sections of the line on the same side as the side with length </math>x<math> on a trapezoid be equal to </math>1<math>.  


Move on to the second-smallest triangle, formed by attaching this triangle with the next trapezoid. Parallel lines give us similar triangles, so we know the proportion of this triangle to the previous triangle is <math>(\frac{x+1}{x})^2</math>. Multiplying, we get <math>(x+1)^2</math> as the area of the triangle, so the area of the trapezoid is <math>2x+1</math>. Repeating this process, we get that the area of B is <math>2x+3</math>, the area of C is <math>2x+7</math>, and the area of D is <math>2x+11</math>.
Move on to the second-smallest triangle, formed by attaching this triangle with the next trapezoid. Parallel lines give us similar triangles, so we know the proportion of this triangle to the previous triangle is </math>(\frac{x+1}{x})^2<math>. Multiplying, we get </math>(x+1)^2<math> as the area of the triangle, so the area of the trapezoid is </math>2x+1<math>. Repeating this process, we get that the area of B is </math>2x+3<math>, the area of C is </math>2x+7<math>, and the area of D is </math>2x+11<math>.


We can now use the given condition that the ratio of C and B is <math>\frac{11}{5}</math>.
We can now use the given condition that the ratio of C and B is </math>\frac{11}{5}<math>.


<math>\frac{11}{5} = \frac{2x+7}{2x+3}</math> gives us <math>x = \frac{1}{6}</math>
</math>\frac{11}{5} = \frac{2x+7}{2x+3}<math> gives us </math>x = \frac{1}{6}<math>


So now we compute the ratio of D and A, which is <math>\frac{2(\frac{1}{6} + 11)}{(\frac{1}{6})^2} = \boxed{408.}</math>
So now we compute the ratio of D and A, which is </math>\frac{2(\frac{1}{6} + 11)}{(\frac{1}{6})^2} = \boxed{408.}$


== See also ==
== See also ==

Revision as of 20:09, 2 July 2020

Problem

An angle is drawn on a set of equally spaced parallel lines as shown. The ratio of the area of shaded region $C$ to the area of shaded region $B$ is 11/5. Find the ratio of shaded region $D$ to the area of shaded region $A$.

Solution 1

Note that the apex of the angle is not on the parallel lines. Set up a coordinate proof.

Let the set of parallel lines be perpendicular to the x-axis, such that they cross it at $0, 1, 2 \ldots$. The base of region $\mathcal{A}$ is on the line $x = 1$. The bigger base of region $\mathcal{D}$ is on the line $x = 7$. Let the top side of the angle be $y = x - s$ and the bottom side be x-axis, as dividing the angle doesn't change the problem.

Since the area of the triangle is equal to $\frac{1}{2}bh$,

Region $C$/Region $B$ = \frac{11}{5} = \frac{\frac 12(5-s)^2 - \frac 12(4-s)^2}{\frac 12(3-s)^2 - \frac12(2-s)^2} $$ (Error compiling LaTeX. Unknown error_msg)

Solve this to find that $s = \frac{5}{6}$.

Using the same reasoning as above, we get Region $D$/Region $A$ = \frac{\frac 12(7-s)^2 - \frac 12(6-s)^2}{\frac 12(1-s)^2}$, which is$\boxed{408}$.

== Solution 2 ==

Note that the sections between the two transversals can be divided into one small triangle and a number of trapezoids. Let one side length (not on a parallel line) of the small triangle be$ (Error compiling LaTeX. Unknown error_msg)x$and the area of it be$x^2$. Also, let all sections of the line on the same side as the side with length$x$on a trapezoid be equal to$1$.

Move on to the second-smallest triangle, formed by attaching this triangle with the next trapezoid. Parallel lines give us similar triangles, so we know the proportion of this triangle to the previous triangle is$ (Error compiling LaTeX. Unknown error_msg)(\frac{x+1}{x})^2$. Multiplying, we get$(x+1)^2$as the area of the triangle, so the area of the trapezoid is$2x+1$. Repeating this process, we get that the area of B is$2x+3$, the area of C is$2x+7$, and the area of D is$2x+11$.

We can now use the given condition that the ratio of C and B is$ (Error compiling LaTeX. Unknown error_msg)\frac{11}{5}$.$\frac{11}{5} = \frac{2x+7}{2x+3}$gives us$x = \frac{1}{6}$So now we compute the ratio of D and A, which is$\frac{2(\frac{1}{6} + 11)}{(\frac{1}{6})^2} = \boxed{408.}$

See also

2006 AIME I (Problems • Answer Key • Resources)
Preceded by
Problem 6 		Followed by
Problem 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America.

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2006_AIME_I_Problems/Problem_7&oldid=127329"