Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2008 AMC 12B Problems/Problem 25: Difference between revisions

← Older editNewer edit →
Bob Smith (talk | contribs)
22 edits
mNo edit summary
Line 12: Line 12:
To simplify things even more, notice that <math>90^{\circ}=\frac{\angle D+\angle A}{2}=180^{\circ}-\angle APD</math>, so <math>\angle P=\angle Q=90^{\circ}</math>.
To simplify things even more, notice that <math>90^{\circ}=\frac{\angle D+\angle A}{2}=180^{\circ}-\angle APD</math>, so <math>\angle P=\angle Q=90^{\circ}</math>.


Also, <cmath>\sin(\angle PDA)=\sin(\frac12\angle XDA)=\sqrt{\frac{1-\cos(\angle XDA)}{2}}=\sqrt{\frac{3}{28}}</cmath>
Also, <cmath>\sin(\angle PAD)=\sin(\frac12\angle XDA)=\sqrt{\frac{1-\cos(\angle XDA)}{2}}=\sqrt{\frac{3}{28}}</cmath>
So the area of <math>\triangle APD</math> is: <cmath>R\cdot c\sin a\sin b =\frac{7\cdot7}{2}\sqrt{\frac{3}{28}}\sqrt{1-\frac{3}{28}}=\frac{35}{8}\sqrt{3}</cmath>
So the area of <math>\triangle APD</math> is: <cmath>R\cdot c\sin a\sin b =\frac{7\cdot7}{2}\sqrt{\frac{3}{28}}\sqrt{1-\frac{3}{28}}=\frac{35}{8}\sqrt{3}</cmath>


Revision as of 10:57, 11 April 2015

Problem 25

Let $ABCD$ be a trapezoid with $AB||CD, AB=11, BC=5, CD=19,$ and $DA=7$. Bisectors of $\angle A$ and $\angle D$ meet at $P$, and bisectors of $\angle B$ and $\angle C$ meet at $Q$. What is the area of hexagon $ABQCDP$?

$\textbf{(A)}\ 28\sqrt{3}\qquad \textbf{(B)}\ 30\sqrt{3}\qquad \textbf{(C)}\ 32\sqrt{3}\qquad \textbf{(D)}\ 35\sqrt{3}\qquad \textbf{(E)}\ 36\sqrt{3}$

Solution

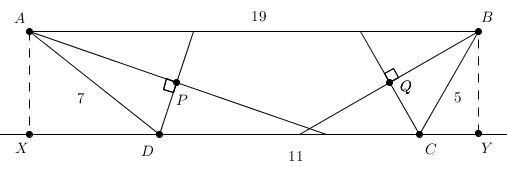
Drop perpendiculars to $CD$ from $A$ and $B$, and call the intersections $X,Y$ respectively. Now, $DA^2-BC^2=(7-5)(7+5)=DX^2-CY^2$ and $DX+CY=19-11=8$. Thus, $DX-CY=3$. We conclude $DX=\frac{11}{2}$ and $CY=\frac{5}{2}$. To simplify things even more, notice that $90^{\circ}=\frac{\angle D+\angle A}{2}=180^{\circ}-\angle APD$, so $\angle P=\angle Q=90^{\circ}$.

Also, \[\sin(\angle PAD)=\sin(\frac12\angle XDA)=\sqrt{\frac{1-\cos(\angle XDA)}{2}}=\sqrt{\frac{3}{28}}\] So the area of $\triangle APD$ is: \[R\cdot c\sin a\sin b =\frac{7\cdot7}{2}\sqrt{\frac{3}{28}}\sqrt{1-\frac{3}{28}}=\frac{35}{8}\sqrt{3}\]

Over to the other side: $\triangle BCY$ is $30-60-90$, and is therefore congruent to $\triangle BCQ$. So $[BCQ]=\frac{5\cdot5\sqrt{3}}{8}$.

The area of the hexagon is clearly $[ABCD]-([BCQ]+[APD])$\[=\frac{15\cdot5\sqrt{3}}{2}-\frac{60\sqrt{3}}{8}=30\sqrt{3}\implies\boxed{B}\]

Alternate Solution

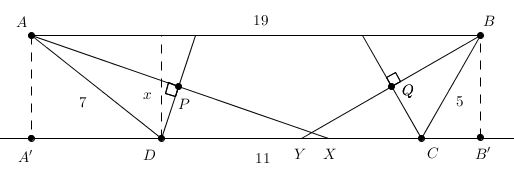
Let $AP$ and $BQ$ meet $CD$ at $X$ and $Y$, respectively.

Since $\angle APD=90^{\circ}$, $\angle ADP=\angle XDP$, and they share $DP$, triangles $APD$ and $XPD$ are congruent.

By the same reasoning, we also have that triangles $BQC$ and $YQC$ are congruent.

Hence, we have $[ABQCDP]=[ABYX]+\frac{[ABCD]-[ABYX]}{2}=\frac{[ABCD]+[ABYX]}{2}$.

If we let the height of the trapezoid be $x$, we have $[ABQCDP]=\frac{\frac{11+19}{2}\cdot x+\frac{11+7}{2}\cdot x}{2}=12x$.

Thusly, if we find the height of the trapezoid and multiply it by 12, we will be done.

Let the projections of $A$ and $B$ to $CD$ be $A'$ and $B'$, respectively.

We have $DA'+CB'=19-11=8$, $DA'=\sqrt{DA^2-AA'^2}=\sqrt{49-x^2}$, and $CB'=\sqrt{CB^2-BB'^2}=\sqrt{25-x^2}$.

Therefore, $\sqrt{49-x^2}+\sqrt{25-x^2}=8$. Solving this, we easily get that $x=\frac{5\sqrt{3}}{2}$.

Multiplying this by 12, we find that the area of hexagon $ABQCDP$ is $30\sqrt{3}$, which corresponds to answer choice $\boxed{B}$.

See Also

2008 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 24 		Followed by
Last Question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America.

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2008_AMC_12B_Problems/Problem_25&oldid=69896"