2018 MPFG Problem 17: Difference between revisions
| Line 12: | Line 12: | ||
<math>\angle ZCX = 15^{\circ} + 75^{\circ} = 90^{\circ}</math> | <math>\angle ZCX = 15^{\circ} + 75^{\circ} = 90^{\circ}</math> | ||
<math>S_{\Delta XYZ} = S_{ACBZ} = S_{\Delta ACB} + S_{\Delta AZB} = 6 + \frac{1}{2} \cdot 5^2 \cdot sin15^{\circ}cos15^{\circ} = 6 + \frac{1}{2} \cdot 5^2 \cdot \frac{1}{2}sin30^{\circ} = 6+\frac{25}{8} = \frac{73}{8}</math> | <math>S_{\Delta XYZ} = S_{ACBZ} = S_{\Delta ACB} + S_{\Delta AZB} = 6 + \frac{1}{2} \cdot 5^2 \cdot sin15^{\circ}cos15^{\circ} = 6 + \frac{1}{2} \cdot 5^2 \cdot \frac{1}{2}sin30^{\circ} = 6+\frac{25}{8} = \boxed{\frac{73}{8}}</math> | ||
~cassphe | |||
Revision as of 11:30, 29 August 2025
Problem
Let ![]() be a triangle with
be a triangle with ![]() ,
, ![]() , and
, and ![]() . On each side of
. On each side of ![]() , externally erect a semicircle whose diameter is the corresponding side. Let
, externally erect a semicircle whose diameter is the corresponding side. Let ![]() be on the semicircular arc erected on side
be on the semicircular arc erected on side ![]() such that
such that ![]() has measure
has measure ![]() . Let
. Let ![]() be on the semicircular arc erected on side
be on the semicircular arc erected on side ![]() such that
such that ![]() has measure
has measure ![]() . Similarly, let
. Similarly, let ![]() be on the semicircular arc erected on side
be on the semicircular arc erected on side ![]() such that
such that ![]() has measure
has measure ![]() . What is the area of triangle
. What is the area of triangle ![]() ? Express your answer as a fraction in simplest form.
? Express your answer as a fraction in simplest form.
Solution 1
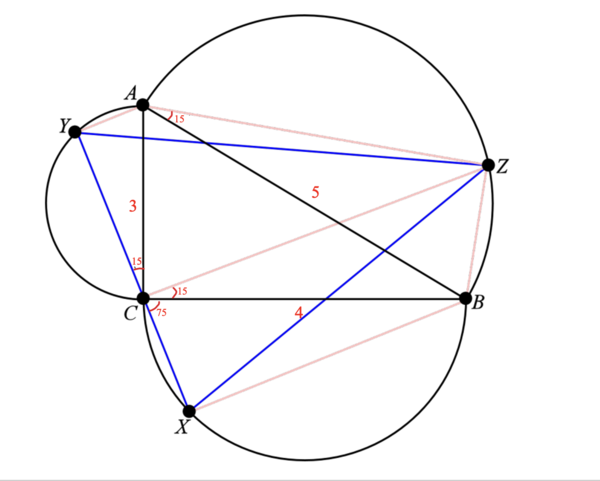
![]() ,
,![]() and
and ![]() is collinear.
is collinear.
Because ![]() ,
, ![]() is concyclic.
is concyclic. ![]()
![]()
![]()
~cassphe









