2013 MPFG Problem 17: Difference between revisions
| Line 13: | Line 13: | ||
As such, <math>f(f(f(x))</math> will have <math>2\cdot4^{2} = 32</math> cycles in the domain <math>[-2,2]</math>. Each has <math>2</math> points that cross with <math>f(x)</math>. However, at <math>3</math> special locations, the crossing points of two consecutive <math>f(f(f(x)))</math> cycles overlapped (at <math>x=-1, 0, 1</math>). | As such, <math>f(f(f(x))</math> will have <math>2\cdot4^{2} = 32</math> cycles in the domain <math>[-2,2]</math>. Each has <math>2</math> points that cross with <math>f(x)</math>. However, at <math>3</math> special locations, the crossing points of two consecutive <math>f(f(f(x)))</math> cycles overlapped (at <math>x=-1, 0, 1</math>). | ||
As such, number of total points is <math>2\cdot32-3 = \boxed{61}</math> | As such, number of total points is <math>2\cdot32-3 = \boxed{61}</math> | ||
～cassphe | |||
Latest revision as of 08:10, 21 August 2025
Problem
Let f be the function defined by 
. How many values of x such that 
satisfy the equation 
?
Solution 1
We first create the graph of 
by transforming a regular 
graph by scaling down 
by 
and scaling up 
by 
.
.jpg)
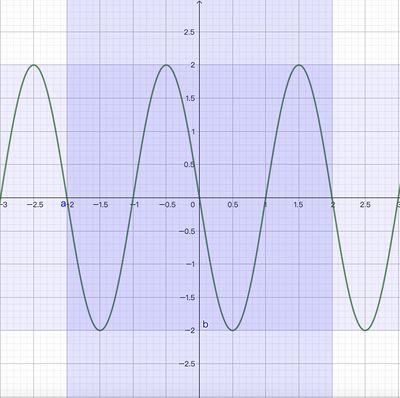
We observe that the domain & range of is restricted in ![$[-2,2]$](http://latex.artofproblemsolving.com/f/6/0/f60010fd01c6801d1b857f1acefb200f1ee8c682.png)
and the graph is restricted in a 
square. Trying out 
, we see that every 
of a cycle of ranges over ![$[0,\pm 2]$](http://latex.artofproblemsolving.com/a/7/b/a7b7dad4fb35e4c2f4d7b9c767ddb8709ebf2446.png)
, which means a cycle for 
will have 
cycles for . and have two crossing points in each small cycle of
).jpg)
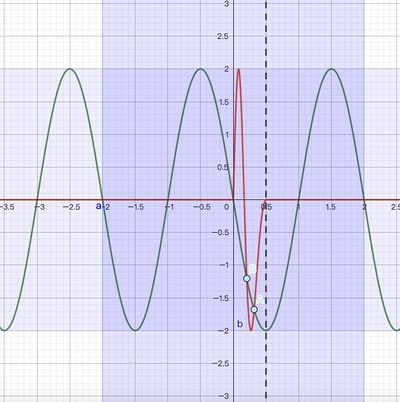
As such, 
will have 
cycles in the domain . Each has 
points that cross with . However, at 
special locations, the crossing points of two consecutive 
cycles overlapped (at 
).
As such, number of total points is 
～cassphe
