Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2004 AMC 12A Problems/Problem 8: Difference between revisions

← Older editNewer edit →
merge
Line 1: Line 1:
{{duplicate|[[2004 AMC 12A Problems|2004 AMC 12A #8]] and [[2004 AMC 10A Problems/Problem 9|2004 AMC 10A #9]]}}
== Problem ==
== Problem ==
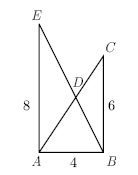
In the overlapping [[triangle]]s <math>\triangle{ABC}</math> and <math>\triangle{ABE}</math> sharing common [[side]] <math>AB</math>, <math>\angle{EAB}</math> and <math>\angle{ABC}</math> are [[right angle]]s, <math>AB=4</math>, <math>BC=6</math>, <math>AE=8</math>, and <math>\overline{AC}</math> and <math>\overline{BE}</math> intersect at <math>D</math>. What is the difference between the areas of <math>\triangle{ADE}</math> and <math>\triangle{BDC}</math>?  
In the overlapping [[triangle]]s <math>\triangle{ABC}</math> and <math>\triangle{ABE}</math> sharing common [[side]] <math>AB</math>, <math>\angle{EAB}</math> and <math>\angle{ABC}</math> are [[right angle]]s, <math>AB=4</math>, <math>BC=6</math>, <math>AE=8</math>, and <math>\overline{AC}</math> and <math>\overline{BE}</math> intersect at <math>D</math>. What is the difference between the areas of <math>\triangle{ADE}</math> and <math>\triangle{BDC}</math>?  
[[Image:AMC10_2004A_9.gif|center]]


<math>\mathrm {(A)}\ 2 \qquad \mathrm {(B)}\ 4 \qquad \mathrm {(C)}\ 5 \qquad \mathrm {(D)}\ 8 \qquad \mathrm {(E)}\ 9 \qquad</math>
<math>\mathrm {(A)}\ 2 \qquad \mathrm {(B)}\ 4 \qquad \mathrm {(C)}\ 5 \qquad \mathrm {(D)}\ 8 \qquad \mathrm {(E)}\ 9 \qquad</math>
Line 6: Line 9:
__TOC__
__TOC__
== Solution ==
== Solution ==
[[Image:2004_AMC12A-8.png]]
=== Solution 1 ===
=== Solution 1 ===
If we let <math>[\ldots]</math> denote area, <math>[ABE] - [ABC] = [ADE] + [ABD] - [ABD] - [BDC] = [ADE] - [BDC]</math>. Using the given, <math>[ABE] = \frac 12 \cdot 8 \cdot 4</math> and <math>[ABC] = \frac 12 \cdot 6 \cdot 4</math>, and their difference is <math>16 - 12 = 4\ \mathrm{(B)}</math>.
If we let <math>[\ldots]</math> denote area, <math>[ABE] - [ABC] = [ADE] + [ABD] - [ABD] - [BDC] = [ADE] - [BDC]</math>. Using the given, <math>[ABE] = \frac 12 \cdot 8 \cdot 4</math> and <math>[ABC] = \frac 12 \cdot 6 \cdot 4</math>, and their difference is <math>16 - 12 = 4\ \mathrm{(B)}</math>.
Line 14: Line 16:


== See also ==
== See also ==
* [http://www.artofproblemsolving.com/Forum/viewtopic.php?t=131320 AoPS topic]
{{AMC12 box|year=2004|ab=A|num-b=7|num-a=9}}
{{AMC12 box|year=2004|ab=A|num-b=7|num-a=9}}
{{AMC10 box|year=2004|ab=A|num-b=8|num-a=10}}


[[Category:Introductory Geometry Problems]]
[[Category:Introductory Geometry Problems]]

Revision as of 20:57, 23 April 2008

The following problem is from both the 2004 AMC 12A #8 and 2004 AMC 10A #9, so both problems redirect to this page.

Problem

In the overlapping triangles $\triangle{ABC}$ and $\triangle{ABE}$ sharing common side $AB$, $\angle{EAB}$ and $\angle{ABC}$ are right angles, $AB=4$, $BC=6$, $AE=8$, and $\overline{AC}$ and $\overline{BE}$ intersect at $D$. What is the difference between the areas of $\triangle{ADE}$ and $\triangle{BDC}$?

$\mathrm {(A)}\ 2 \qquad \mathrm {(B)}\ 4 \qquad \mathrm {(C)}\ 5 \qquad \mathrm {(D)}\ 8 \qquad \mathrm {(E)}\ 9 \qquad$

Solution

Solution 1

If we let $[\ldots]$ denote area, $[ABE] - [ABC] = [ADE] + [ABD] - [ABD] - [BDC] = [ADE] - [BDC]$. Using the given, $[ABE] = \frac 12 \cdot 8 \cdot 4$ and $[ABC] = \frac 12 \cdot 6 \cdot 4$, and their difference is $16 - 12 = 4\ \mathrm{(B)}$.

Solution 2

Since $AE \perp AB$ and $BC \perp AB$, $AE \parallel BC$. By alternate interior angles and AA~, we find that $\triangle ADE \sim \triangle CDB$, with side length ratio $\frac{4}{3}$. Their heights also have the same ratio, and since the two heights add up to $4$, we have that $h_{ADE} = 4 \cdot \frac{4}{7} = \frac{16}{7}$ and $h_{CDB} = 3 \cdot \frac 47 = \frac {12}7$. Subtracting the areas, $\frac{1}{2} \cdot 8 \cdot \frac {16}7 - \frac 12 \cdot 6 \cdot \frac{12}7 = 4$.

See also

2004 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 7 		Followed by
Problem 9
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions
2004 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 8 		Followed by
Problem 10
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2004_AMC_12A_Problems/Problem_8&oldid=25220"