Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2005 AMC 12A Problems/Problem 15: Difference between revisions

Newer edit →
solution
 
rmv img, \sim
Line 4: Line 4:
<math>(\text {A}) \ \frac {1}{6} \qquad (\text {B}) \ \frac {1}{4} \qquad (\text {C})\ \frac {1}{3} \qquad (\text {D}) \ \frac {1}{2} \qquad (\text {E})\ \frac {2}{3}</math>
<math>(\text {A}) \ \frac {1}{6} \qquad (\text {B}) \ \frac {1}{4} \qquad (\text {C})\ \frac {1}{3} \qquad (\text {D}) \ \frac {1}{2} \qquad (\text {E})\ \frac {2}{3}</math>


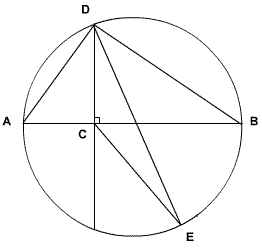
[[Image:2005_12A_AMC-15.png]] (Upload from [http://www.artofproblemsolving.com/Forum/viewtopic.php?p=368491#368491])
[[Image:2005_12A_AMC-15.png]]  


== Solution ==
== Solution ==
Line 11: Line 11:
Call the radius <math>r</math>. Then <math>AC = \frac 13(2r) = \frac 23r</math>, <math>CO = \frac 13r</math>. Using the [[Pythagorean Theorem]] in <math>\triangle OCD</math>, we get <math>\frac{1}{3}r^2 + CD^2 = r^2 \Longrightarrow CD = \frac{2\sqrt{2}}3r</math>.  
Call the radius <math>r</math>. Then <math>AC = \frac 13(2r) = \frac 23r</math>, <math>CO = \frac 13r</math>. Using the [[Pythagorean Theorem]] in <math>\triangle OCD</math>, we get <math>\frac{1}{3}r^2 + CD^2 = r^2 \Longrightarrow CD = \frac{2\sqrt{2}}3r</math>.  


Now we have to find <math>CF</math>. Notice <math>\triangle OCD \similar \triangle OFC</math>, so we can write the [[proportion]]:
Now we have to find <math>CF</math>. Notice <math>\triangle OCD \sim \triangle OFC</math>, so we can write the [[proportion]]:


<div style="text-align:center;"><math>\frac{OF}{OC} = \frac{OC}{OD}</math><br /><math>\frac{OF}{\frac{1}{3}r} = \frac{\frac{1}{3}r}{r}</math><br /><math>OF = \frac 19r</math></div>
<div style="text-align:center;"><math>\frac{OF}{OC} = \frac{OC}{OD}</math><br /><math>\frac{OF}{\frac{1}{3}r} = \frac{\frac{1}{3}r}{r}</math><br /><math>OF = \frac 19r</math></div>
Line 22: Line 22:
{{AMC12 box|year=2005|num-b=14|num-a=16|ab=A}}
{{AMC12 box|year=2005|num-b=14|num-a=16|ab=A}}


{{image}}
[[Category:Introductory Geometry Problems]]
[[Category:Introductory Geometry Problems]]

Revision as of 14:19, 23 September 2007

Problem

Let $\overline{AB}$ be a diameter of a circle and $C$ be a point on $\overline{AB}$ with $2 \cdot AC = BC$. Let $D$ and $E$ be points on the circle such that $\overline{DC} \perp \overline{AB}$ and $\overline{DE}$ is a second diameter. What is the ratio of the area of $\triangle DCE$ to the area of $\triangle ABD$?

$(\text {A}) \ \frac {1}{6} \qquad (\text {B}) \ \frac {1}{4} \qquad (\text {C})\ \frac {1}{3} \qquad (\text {D}) \ \frac {1}{2} \qquad (\text {E})\ \frac {2}{3}$

Solution

Notice that the bases of both triangles are diameters of the circle. Hence the ratio of the areas is just the ratio of the heights of the triangles, or $\frac{CD}{CF}$ ($F$ is the foot of the perpendicular from $C$ to $DE$).

Call the radius $r$. Then $AC = \frac 13(2r) = \frac 23r$, $CO = \frac 13r$. Using the Pythagorean Theorem in $\triangle OCD$, we get $\frac{1}{3}r^2 + CD^2 = r^2 \Longrightarrow CD = \frac{2\sqrt{2}}3r$.

Now we have to find $CF$. Notice $\triangle OCD \sim \triangle OFC$, so we can write the proportion:

$\frac{OF}{OC} = \frac{OC}{OD}$
$\frac{OF}{\frac{1}{3}r} = \frac{\frac{1}{3}r}{r}$
$OF = \frac 19r$

By the Pythagorean Theorem in $\triangle OFC$, we have $\left(\frac{1}{9}r\right)^2 + CF^2 = \left(\frac{1}{3}r\right)^2 \Longrightarrow CF = \sqrt{\frac{8}{81}r^2} = \frac{2\sqrt{2}}{9}r$.

Our answer is $\frac{CD}{CF} = \frac{\frac{2\sqrt{2}}{3}r}{\frac{2\sqrt{2}}{9}r} = \frac 13 \Longrightarrow \mathrm{(C)}$.

See also

2005 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Problem 16
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions
Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2005_AMC_12A_Problems/Problem_15&oldid=16633"