2021 JMPSC Accuracy Problems/Problem 12: Difference between revisions
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
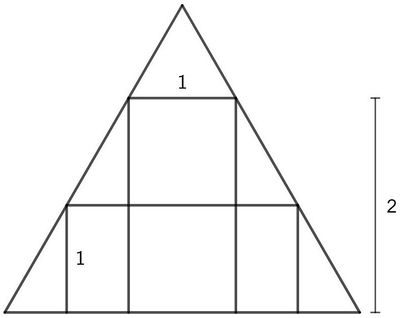
A rectangle with base <math>1</math> and height <math>2</math> is inscribed in an equilateral triangle. Another rectangle with height <math>1</math> is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction <math>\frac{a+b\sqrt{3}}{c}</math> such that <math>gcd(a,b,c)=1.</math> Find <math>a+b+c</math>. | A rectangle with base <math>1</math> and height <math>2</math> is inscribed in an equilateral triangle. Another rectangle with height <math>1</math> is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction <math>\frac{a+b\sqrt{3}}{c}</math> such that <math>gcd(a,b,c)=1.</math> Find <math>a+b+c</math>. | ||
<center> | <center> | ||
[[File:Sprint13.jpg|400px]] | [[File:Sprint13.jpg|400px]] | ||
Revision as of 20:47, 10 July 2021
Problem
A rectangle with base 
and height 
is inscribed in an equilateral triangle. Another rectangle with height is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction 
such that 
Find 
.
Solution
asdf
