2014 AMC 12B Problems/Problem 24: Difference between revisions
XXQw3rtyXx (talk | contribs) |
|||
| (35 intermediate revisions by 9 users not shown) | |||
| Line 8: | Line 8: | ||
\textbf{(E) }421\qquad</math> | \textbf{(E) }421\qquad</math> | ||
==Solution== | == Solution 1 == | ||
Let <math>BE=a</math>, <math>AD=b</math>, and <math>AC=CE=BD=c</math>. Let <math>F</math> be on <math>AE</math> such that <math>CF \perp AE</math>. | |||
<asy> | |||
size(200); | |||
defaultpen(linewidth(0.4)+fontsize(10)); | |||
pen s = linewidth(0.8)+fontsize(8); | |||
pair O,A,B,C,D,E0,F; | |||
O=origin; | |||
A= dir(198); | |||
path c = CR(O,1); | |||
real r = 0.13535; | |||
B = IP(c, CR(A,3*r)); | |||
C = IP(c, CR(B,10*r)); | |||
D = IP(c, CR(C,3*r)); | |||
E0 = OP(c, CR(D,10*r)); | |||
F = foot(C,A,E0); | |||
The sum of the | dot("$A$", A, A-O); | ||
dot("$B$", B, B-O); | |||
dot("$C$", C, C-O); | |||
dot("$D$", D, D-O); | |||
dot("$E$", E0, E0-O); | |||
dot("$F$", F, F-C); | |||
label("$c$",A--C,S); | |||
label("$c$",E0--C,W); | |||
label("$7$",F--E0,S); | |||
label("$7$",F--A,S); | |||
label("$3$",A--B,2*W); | |||
label("$10$",B--C,2*N); | |||
label("$3$",C--D,2*NE); | |||
label("$10$",D--E0,E); | |||
draw(A--B--C--D--E0--A, black+0.8); | |||
draw(CR(O,1), s); | |||
draw(A--C--E0, royalblue); | |||
draw(C--F, royalblue+dashed); | |||
draw(rightanglemark(E0,F,C,2)); | |||
MA("\theta",A,B,C,0.075); | |||
MA("\pi-\theta",C,E0,A,0.1); | |||
</asy> | |||
In <math>\triangle CFE</math> we have <math>\cos\theta = -\cos(\pi-\theta)=-7/c</math>. We use the [[Law of Cosines]] on <math>\triangle ABC</math> to get <math>60\cos\theta = 109-c^2</math>. Eliminating <math>\cos\theta</math> we get <math>c^3-109c-420=0</math> which factorizes as | |||
<cmath>(c+7)(c+5)(c-12)=0.</cmath>Discarding the negative roots we have <math>c=12</math>. Thus <math>BD=AC=CE=12</math>. For <math>BE=a</math>, we use Ptolemy's theorem on cyclic quadrilateral <math>ABCE</math> to get <math>a=44/3</math>. For <math>AD=b</math>, we use [[Ptolemy's theorem]] on cyclic quadrilateral <math>ACDE</math> to get <math>b=27/2</math>. | |||
The sum of the lengths of the diagonals is <math>12+12+12+\tfrac{44}{3}+\tfrac{27}{2} = \tfrac{385}{6}</math> so the answer is <math>385 + 6 = \fbox{\textbf{(D) }391}</math> | |||
== Solution 2 == | |||
Let <math>a</math> denote the length of a diagonal opposite adjacent sides of length <math>14</math> and <math>3</math>, <math>b</math> for sides <math>14</math> and <math>10</math>, and <math>c</math> for sides <math>3</math> and <math>10</math>. Using Ptolemy's Theorem on the five possible quadrilaterals in the configuration, we obtain: | |||
<cmath> | |||
\begin{align} | |||
c^2 &= 3a+100 \\ | |||
c^2 &= 10b+9 \\ | |||
ab &= 30+14c \\ | |||
ac &= 3c+140\\ | |||
bc &= 10c+42 | |||
\end{align} | |||
</cmath> | |||
Using equations <math>(1)</math> and <math>(2)</math>, we obtain: | |||
<cmath> | |||
a = \frac{c^2-100}{3} | |||
</cmath> | |||
and | |||
<cmath> | |||
b = \frac{c^2-9}{10} | |||
</cmath> | |||
Plugging into equation <math>(4)</math>, we find that: | |||
<cmath> | |||
\begin{align*} | |||
\frac{c^2-100}{3}c &= 3c + 140\\ | |||
\frac{c^3-100c}{3} &= 3c + 140\\ | |||
c^3-100c &= 9c + 420\\ | |||
c^3-109c-420 &=0\\ | |||
(c-12)(c+7)(c+5)&=0 | |||
\end{align*} | |||
</cmath> | |||
Or similarly into equation <math>(5)</math> to check: | |||
<cmath> | |||
\begin{align*} | |||
\frac{c^2-9}{10}c &= 10c+42\\ | |||
\frac{c^3-9c}{10} &= 10c + 42\\ | |||
c^3-9c &= 100c + 420\\ | |||
c^3-109c-420 &=0\\ | |||
(c-12)(c+7)(c+5)&=0 | |||
\end{align*} | |||
</cmath> | |||
<math>c</math>, being a length, must be positive, implying that <math>c=12</math>. In fact, this is reasonable, since <math>10+3\approx 12</math> in the pentagon with apparently obtuse angles. Plugging this back into equations <math>(1)</math> and <math>(2)</math> we find that <math>a = \frac{44}{3}</math> and <math>b= \frac{135}{10}=\frac{27}{2}</math>. | |||
We desire <math>3c+a+b = 3\cdot 12 + \frac{44}{3} + \frac{27}{2} = \frac{216+88+81}{6}=\frac{385}{6}</math>, so it follows that the answer is <math>385 + 6 = \fbox{\textbf{(D) }391}</math> | |||
==Solution 3 (Ptolemy's but Quicker)== | |||
Let us set <math>x</math> to be <math>AC=BD=CE</math> and <math>y</math> to be <math>BE</math> and <math>z</math> to be <math>AD</math>. It follow from applying [[Ptolemy's Theorem]] on <math>ABCD</math> to get <math>x^2=9+10z</math>. Applying Ptolemy's on <math>ACDE</math> gives <math>xz=42+10x</math>; and applying Ptolemy's on <math>BCDE</math> gives <math>x^2=100+3y</math>. So, we have the have the following system of equations: | |||
<cmath> | |||
\begin{align} | |||
x^2 &= 9+10z \\ | |||
x^2 &= 100+3y \\ | |||
xz &= 42+10x | |||
\end{align} | |||
</cmath> | |||
From <math>(3)</math>, we have <math>42=(z-10)x</math>. Isolating the x gives <math>x=\dfrac{42}{z-10}</math>. Plugging in <math>x=\dfrac{42}{z-10}</math> to <math>(1)</math> gives | |||
<cmath> | |||
\begin{align*} | |||
\left(\frac{42}{z-10}\right)^2 &= 10z+9\\ | |||
10z^3 - 191z^2 + 820z + 900 &= 1764\\ | |||
10z^3 - 191z^2 + 820z - 864 &= 0\\ | |||
(5z-8)(2z-27)(z-4) &=0 | |||
\end{align*} | |||
</cmath> | |||
It is impossible for <math>z<10</math> for <math>x<0</math>; that means <math>z=\frac{27}{2}</math>. That means <math>x = 12</math> and <math>y = \frac{44}{3}</math>. | |||
Thus, the sum of all diagonals is <math>3x+y+z = 3\cdot 12 + \frac{44}{3} + \frac{27}{2} = 385/6</math>, which implies our answer is <math>m+n = 385+6 = \fbox{391 \textbf{(D)}}</math>. | |||
~sml1809 | |||
==Solution 4== | |||
[[File:2014AMC12BProblem24Solution4.png|center|400px]] | |||
Let <math>BE = a</math>, <math>AC = CE = BD = b</math> | |||
By [[Ptolemy's theorem]] for quadrilateral <math>ABCE</math>, <math>AB \cdot CE + BC \cdot AE = BE \cdot AC</math>, <math>3b + 140 = ab</math>, <math>a = 3 + \frac{140}{b}</math> | |||
By [[Ptolemy's theorem]] for quadrilateral <math>BCDE</math>, <math>CD \cdot BE + BC \cdot DE = BD \cdot CE</math>, <math>3a + 100 = b^2</math> | |||
<math>3(3 + \frac{140}{b}) + 100 = b^2</math>, <math>b^3 - 109 b -420 = 0</math>, <math>(b-12)(b+7)(b+5) = 0</math>, <math>b = 12</math> | |||
<math>a = 3 + \frac{140}{12} = \frac{44}{3}</math> | |||
By [[Ptolemy's theorem]] for quadrilateral <math>ABDE</math>, <math>AE \cdot BD + AB \cdot DE = AD \cdot BE</math>, <math>AD \cdot a = 14b + 30</math>, <math>AD = \frac{27}{2}</math> | |||
<math>\frac{m}{n} = 12 + 12 + 12 + \frac{44}{3} + \frac{27}{2} = \frac{385}{6}</math>, <math>385 + 6 = \boxed{\textbf{(D) }391}</math> | |||
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen] | |||
== See also == | == See also == | ||
{{AMC12 box|year=2014|ab=B|num-b=23|num-a=25}} | {{AMC12 box|year=2014|ab=B|num-b=23|num-a=25}} | ||
[[Category:Intermediate Geometry Problems]] | |||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 20:53, 24 September 2025
Problem
Let ![]() be a pentagon inscribed in a circle such that
be a pentagon inscribed in a circle such that ![]() ,
, ![]() , and
, and ![]() . The sum of the lengths of all diagonals of
. The sum of the lengths of all diagonals of ![]() is equal to
is equal to ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. What is
are relatively prime positive integers. What is ![]() ?
?
![]()
Solution 1
Let ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() be on
be on ![]() such that
such that ![]() .
.
![[asy] size(200); defaultpen(linewidth(0.4)+fontsize(10)); pen s = linewidth(0.8)+fontsize(8); pair O,A,B,C,D,E0,F; O=origin; A= dir(198); path c = CR(O,1); real r = 0.13535; B = IP(c, CR(A,3*r)); C = IP(c, CR(B,10*r)); D = IP(c, CR(C,3*r)); E0 = OP(c, CR(D,10*r)); F = foot(C,A,E0); dot("$A$", A, A-O); dot("$B$", B, B-O); dot("$C$", C, C-O); dot("$D$", D, D-O); dot("$E$", E0, E0-O); dot("$F$", F, F-C); label("$c$",A--C,S); label("$c$",E0--C,W); label("$7$",F--E0,S); label("$7$",F--A,S); label("$3$",A--B,2*W); label("$10$",B--C,2*N); label("$3$",C--D,2*NE); label("$10$",D--E0,E); draw(A--B--C--D--E0--A, black+0.8); draw(CR(O,1), s); draw(A--C--E0, royalblue); draw(C--F, royalblue+dashed); draw(rightanglemark(E0,F,C,2)); MA("\theta",A,B,C,0.075); MA("\pi-\theta",C,E0,A,0.1); [/asy]](http://latex.artofproblemsolving.com/f/3/0/f309928844b6dc47e0410382e86dd44b9cf39966.png) In
In ![]() we have
we have ![]() . We use the Law of Cosines on
. We use the Law of Cosines on ![]() to get
to get ![]() . Eliminating
. Eliminating ![]() we get
we get ![]() which factorizes as
which factorizes as
![]() Discarding the negative roots we have
Discarding the negative roots we have ![]() . Thus
. Thus ![]() . For
. For ![]() , we use Ptolemy's theorem on cyclic quadrilateral
, we use Ptolemy's theorem on cyclic quadrilateral ![]() to get
to get ![]() . For
. For ![]() , we use Ptolemy's theorem on cyclic quadrilateral
, we use Ptolemy's theorem on cyclic quadrilateral ![]() to get
to get ![]() .
.
The sum of the lengths of the diagonals is ![]() so the answer is
so the answer is ![]()
Solution 2
Let ![]() denote the length of a diagonal opposite adjacent sides of length
denote the length of a diagonal opposite adjacent sides of length ![]() and
and ![]() ,
, ![]() for sides
for sides ![]() and
and ![]() , and
, and ![]() for sides
for sides ![]() and
and ![]() . Using Ptolemy's Theorem on the five possible quadrilaterals in the configuration, we obtain:
. Using Ptolemy's Theorem on the five possible quadrilaterals in the configuration, we obtain:

Using equations ![]() and
and ![]() , we obtain:
, we obtain:
![]()
and
![]()
Plugging into equation ![]() , we find that:
, we find that:

Or similarly into equation ![]() to check:
to check:

![]() , being a length, must be positive, implying that
, being a length, must be positive, implying that ![]() . In fact, this is reasonable, since
. In fact, this is reasonable, since ![]() in the pentagon with apparently obtuse angles. Plugging this back into equations
in the pentagon with apparently obtuse angles. Plugging this back into equations ![]() and
and ![]() we find that
we find that ![]() and
and ![]() .
.
We desire ![]() , so it follows that the answer is
, so it follows that the answer is ![]()
Solution 3 (Ptolemy's but Quicker)
Let us set ![]() to be
to be ![]() and
and ![]() to be
to be ![]() and
and ![]() to be
to be ![]() . It follow from applying Ptolemy's Theorem on
. It follow from applying Ptolemy's Theorem on ![]() to get
to get ![]() . Applying Ptolemy's on
. Applying Ptolemy's on ![]() gives
gives ![]() ; and applying Ptolemy's on
; and applying Ptolemy's on ![]() gives
gives ![]() . So, we have the have the following system of equations:
. So, we have the have the following system of equations:

From ![]() , we have
, we have ![]() . Isolating the x gives
. Isolating the x gives ![]() . Plugging in
. Plugging in ![]() to
to ![]() gives
gives

It is impossible for ![]() for
for ![]() ; that means
; that means ![]() . That means
. That means ![]() and
and ![]() .
.
Thus, the sum of all diagonals is ![]() , which implies our answer is
, which implies our answer is ![]() .
.
~sml1809
Solution 4
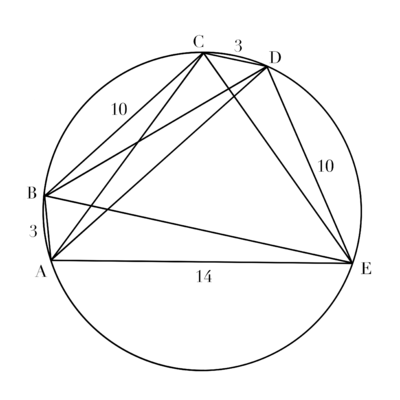
Let ![]() ,
, ![]()
By Ptolemy's theorem for quadrilateral ![]() ,
, ![]() ,
, ![]() ,
, ![]()
By Ptolemy's theorem for quadrilateral ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
By Ptolemy's theorem for quadrilateral ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
See also
| 2014 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 23 |
Followed by Problem 25 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
These problems are copyrighted © by the Mathematical Association of America. 









