Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2024 AMC 10B Problems/Problem 10: Difference between revisions

← Older edit
Lanny2023 (talk | contribs)
editor
5 edits
Zhixing (talk | contribs)
editor
101 edits
Undo revision 267843 by Lanny2023 (talk)
 
Line 1: Line 1:
67676767767676767
==Problem==
Quadrilateral <imath>ABCD</imath> is a parallelogram, and <imath>E</imath> is the midpoint of the side <imath>\overline{AD}</imath>. Let <imath>F</imath> be the intersection of lines <imath>EB</imath> and <imath>AC</imath>. What is the ratio of the area of
quadrilateral <imath>CDEF</imath> to the area of <imath>\triangle CFB</imath>?
 
<imath>\textbf{(A) } 5:4 \qquad\textbf{(B) } 4:3 \qquad\textbf{(C) } 3:2 \qquad\textbf{(D) } 5:3 \qquad\textbf{(E) } 2:1</imath>


==Solution 1==
==Solution 1==
Let <math>AB = CD</math> have length <math>b</math> and let the altitude of the parallelogram perpendicular to <math>\overline{AD}</math> have length <math>h</math>.
Let <imath>AB = CD</imath> have length <imath>b</imath> and let the altitude of the parallelogram perpendicular to <imath>\overline{AD}</imath> have length <imath>h</imath>.


The area of the parallelogram is <math>bh</math> and the area of <math>\triangle ABE</math> equals <math>\frac{(b/2)(h)}{2} = \frac{bh}{4}</math>. Thus, the area of quadrilateral <math>BCDE</math> is <math>bh - \frac{bh}{4} = \frac{3bh}{4}</math>.
The area of the parallelogram is <imath>bh</imath> and the area of <imath>\triangle ABE</imath> equals <imath>\frac{(b/2)(h)}{2} = \frac{bh}{4}</imath>. Thus, the area of quadrilateral <imath>BCDE</imath> is <imath>bh - \frac{bh}{4} = \frac{3bh}{4}</imath>.


We have from <math>AA</math> that <math>\triangle CBF \sim \triangle AEF</math>. Also, <math>CB/AE = 2</math>, so the length of the altitude of <math>\triangle CBF</math> from <math>F</math> is twice that of <math>\triangle AEF</math>. This means that the altitude of <math>\triangle CBF</math> is <math>2h/3</math>, so the area of <math>\triangle CBF</math> is <math>\frac{(b)(2h/3)}{2} = \frac{bh}{3}</math>.
We have from <imath>AA</imath> that <imath>\triangle CBF \sim \triangle AEF</imath>. Also, <imath>CB/AE = 2</imath>, so the length of the altitude of <imath>\triangle CBF</imath> from <imath>F</imath> is twice that of <imath>\triangle AEF</imath>. This means that the altitude of <imath>\triangle CBF</imath> is <imath>2h/3</imath>, so the area of <imath>\triangle CBF</imath> is <imath>\frac{(b)(2h/3)}{2} = \frac{bh}{3}</imath>.


Then, the area of quadrilateral <math>CDEF</math> equals the area of <math>BCDE</math> minus that of <math>\triangle CBF</math>, which is <math>\frac{3bh}{4} - \frac{bh}{3} = \frac{5bh}{12}</math>. Finally, the ratio of the area of <math>CDEF</math> to the area of triangle <math>CFB</math> is <math>\frac{\frac{5bh}{12}}{\frac{bh}{3}} = \frac{\frac{5}{12}}{\frac{1}{3}} = \frac{5}{4}</math>, so the answer is <math>\boxed{\textbf{(A) } 5:4}</math>.
Then, the area of quadrilateral <imath>CDEF</imath> equals the area of <imath>BCDE</imath> minus that of <imath>\triangle CBF</imath>, which is <imath>\frac{3bh}{4} - \frac{bh}{3} = \frac{5bh}{12}</imath>. Finally, the ratio of the area of <imath>CDEF</imath> to the area of triangle <imath>CFB</imath> is <imath>\frac{\frac{5bh}{12}}{\frac{bh}{3}} = \frac{\frac{5}{12}}{\frac{1}{3}} = \frac{5}{4}</imath>, so the answer is <imath>\boxed{\textbf{(A) } 5:4}</imath>.


[[File:2024 AMC 10B 10.png|300px|right]]
[[File:2024 AMC 10B 10.png|300px|right]]
==Solution 2==
==Solution 2==
Let <math>[AFE]=1</math>. Since <math>\triangle AFE\sim\triangle CFB</math> with a scale factor of <math>2</math>, <math>[CFB]=4</math>. The scale factor of <math>2</math> also means that <math>\dfrac{AF}{FC}=\dfrac{1}{2}</math>, therefore since <math>\triangle BCF</math> and <math>\triangle BFA</math> have the same height, <math>[BFA]=2</math>. Since <math>ABCD</math> is a parallelogram, <cmath>[BCA]=[DAC]\implies4+2=1+[CDEF]\implies [CDEF]=5\implies\boxed{\text{(A) }5:4}</cmath>
Let <imath>[AFE]=1</imath>. Since <imath>\triangle AFE\sim\triangle CFB</imath> with a scale factor of <imath>2</imath>, <imath>[CFB]=4</imath>. The scale factor of <imath>2</imath> also means that <imath>\dfrac{AF}{FC}=\dfrac{1}{2}</imath>, therefore since <imath>\triangle BCF</imath> and <imath>\triangle BFA</imath> have the same height, <imath>[BFA]=2</imath>. Since <imath>ABCD</imath> is a parallelogram, <cmath>[BCA]=[DAC]\implies4+2=1+[CDEF]\implies [CDEF]=5\implies\boxed{\text{(A) }5:4}</cmath>


'''vladimir.shelomovskii@gmail.com, vvsss'''
'''vladimir.shelomovskii@gmail.com, vvsss'''


==Solution 3 (Techniques)==
==Solution 3 (Techniques)==
We assert that <math>ABCD</math> is a square of side length <math>6</math>. Notice that <math>\triangle AFE\sim\triangle CFB</math> with a scale factor of <math>2</math>. Since the area of <math>\triangle ABC</math> is <math>18 \implies</math> the area of <math>\triangle CFB</math> is <math>12</math>, so the area of <math>\triangle AFE</math> is <math>3</math>. Thus the area of <math>CDEF</math> is <math>18-3=15</math>, and we conclude that the answer is <math>\frac{15}{12}\implies\boxed{\text{(A) }5:4}</math>
We assert that <imath>ABCD</imath> is a square of side length <imath>6</imath>. Notice that <imath>\triangle AFE\sim\triangle CFB</imath> with a scale factor of <imath>2</imath>. Since the area of <imath>\triangle ABC</imath> is <imath>18 \implies</imath> the area of <imath>\triangle CFB</imath> is <imath>12</imath>, so the area of <imath>\triangle AFE</imath> is <imath>3</imath>. Thus the area of <imath>CDEF</imath> is <imath>18-3=15</imath>, and we conclude that the answer is <imath>\frac{15}{12}\implies\boxed{\text{(A) }5:4}</imath>


  ~Tacos_are_yummy_1
  ~Tacos_are_yummy_1


==Solution 4==
==Solution 4==
Let <math>ABCE</math> be a square with side length <math>1</math>, to assist with calculations. We can put this on the coordinate plane with the points <math>D = (0,0)</math>, <math>C = (1, 0)</math>, <math>B = (1, 1)</math>, and <math>A = (0, 1)</math>. We have <math>E = (0, 0.5)</math>. Therefore, the line <math>EB</math> has slope <math>0.5</math> and y-intercept <math>0.5</math>. The equation of the line is then <math>y = 0.5x + 0.5</math>. The equation of line <math>AC</math> is <math>y = -x + 1</math>. The intersection is when the lines are equal to each other, so we solve the equation. <math>0.5x + 0.5 = -x + 1</math>, so <math>x = \frac{1}{3}</math>. Therefore, plugging it into the equation, we get <math>y= \frac{2}{3}</math>. Using the shoelace theorem, we get the area of <math>CDEF</math> to be <math>\frac{5}{12}</math> and the area of <math>CFB</math> to be <math>\frac{1}{3}</math>, so our ratio is <math>\frac{\frac{5}{12}}{\frac{1}{3}} = \boxed{(A) 5:4}</math> ~idk12345678
Let <imath>ABCE</imath> be a square with side length <imath>1</imath>, to assist with calculations. We can put this on the coordinate plane with the points <imath>D = (0,0)</imath>, <imath>C = (1, 0)</imath>, <imath>B = (1, 1)</imath>, and <imath>A = (0, 1)</imath>. We have <imath>E = (0, 0.5)</imath>. Therefore, the line <imath>EB</imath> has slope <imath>0.5</imath> and y-intercept <imath>0.5</imath>. The equation of the line is then <imath>y = 0.5x + 0.5</imath>. The equation of line <imath>AC</imath> is <imath>y = -x + 1</imath>. The intersection is when the lines are equal to each other, so we solve the equation. <imath>0.5x + 0.5 = -x + 1</imath>, so <imath>x = \frac{1}{3}</imath>. Therefore, plugging it into the equation, we get <imath>y= \frac{2}{3}</imath>. Using the shoelace theorem, we get the area of <imath>CDEF</imath> to be <imath>\frac{5}{12}</imath> and the area of <imath>CFB</imath> to be <imath>\frac{1}{3}</imath>, so our ratio is <imath>\frac{\frac{5}{12}}{\frac{1}{3}} = \boxed{(A) 5:4}</imath> ~idk12345678


==Solution 5 (wlog)==
==Solution 5 (wlog)==
Let <math>ABCE</math> be a square with side length <math>2</math>. We see that <math>\triangle AFE \sim \triangle CFB</math> by a Scale factor of <math>2</math>. Let the altitude of <math>\triangle AFE</math> and altitude of <math>\triangle CFB</math> be <math>h</math> and <math>2h</math>, respectively. We know that <math>h+2h</math> is equal to <math>2</math>, as the height of the square is <math>2</math>. Solving this equation, we get that <math>h = \frac{2}3.</math> This means <math>[\triangle CFB] = \frac{4}3,</math> we can also calculate the area of <math>\triangle ABE</math>. Adding the area we of <math>\triangle CFB</math> and <math>\triangle ABE</math> we get <math>\frac{7}3.</math> We can then subtract this from the total area of the square: <math>4</math>, this gives us <math>\frac{5}3</math> for the area of quadrilateral <math>CFED.</math> Then we can compute the ratio which is equal to <math>\boxed{\textbf{(A) } 5:4}.</math>
Let <imath>ABCE</imath> be a square with side length <imath>2</imath>. We see that <imath>\triangle AFE \sim \triangle CFB</imath> by a Scale factor of <imath>2</imath>. Let the altitude of <imath>\triangle AFE</imath> and altitude of <imath>\triangle CFB</imath> be <imath>h</imath> and <imath>2h</imath>, respectively. We know that <imath>h+2h</imath> is equal to <imath>2</imath>, as the height of the square is <imath>2</imath>. Solving this equation, we get that <imath>h = \frac{2}3.</imath> This means <imath>[\triangle CFB] = \frac{4}3,</imath> we can also calculate the area of <imath>\triangle ABE</imath>. Adding the area we of <imath>\triangle CFB</imath> and <imath>\triangle ABE</imath> we get <imath>\frac{7}3.</imath> We can then subtract this from the total area of the square: <imath>4</imath>, this gives us <imath>\frac{5}3</imath> for the area of quadrilateral <imath>CFED.</imath> Then we can compute the ratio which is equal to <imath>\boxed{\textbf{(A) } 5:4}.</imath>


~yuvag  
~yuvag  


(why does the <math>\LaTeX</math> always look so bugged.)
(why does the <imath>\LaTeX</imath> always look so bugged.)


==Solution 6 (barycentrics)==
==Solution 6 (barycentrics)==
<math>A=(1,0,0), B=(0,1,0), C=(0,0,1), D=(1,-1,1)</math>. Since <math>E</math> is the midpoint of <math>\overline{AD}</math>, <math>E=(1,-0.5,0.5)</math>. The equation of <math>\overline{EB}</math> is:
<imath>A=(1,0,0), B=(0,1,0), C=(0,0,1), D=(1,-1,1)</imath>. Since <imath>E</imath> is the midpoint of <imath>\overline{AD}</imath>, <imath>E=(1,-0.5,0.5)</imath>. The equation of <imath>\overline{EB}</imath> is:
<cmath>
<cmath>
0 =
0 =
Line 41: Line 45:
\end{vmatrix}
\end{vmatrix}
</cmath>
</cmath>
The equation of <math>\overline{AC}</math> is:
The equation of <imath>\overline{AC}</imath> is:
<cmath>
<cmath>
0 =
0 =
Line 50: Line 54:
\end{vmatrix}
\end{vmatrix}
</cmath>
</cmath>
We also know that <math>x+y+z=1</math>. To find the intersection, we can solve the system of equations. Solving, we get <math>x=2/3,y=0,z=1/3</math>. Therefore, <math>F=\left(\frac{2}{3}, 0, \frac{1}{3}\right)</math>. Using barycentric area formula,
We also know that <imath>x+y+z=1</imath>. To find the intersection, we can solve the system of equations. Solving, we get <imath>x=2/3,y=0,z=1/3</imath>. Therefore, <imath>F=\left(\frac{2}{3}, 0, \frac{1}{3}\right)</imath>. Using barycentric area formula,
<cmath>
<cmath>
\frac{[CFB]}{[ABC]} =  
\frac{[CFB]}{[ABC]} =  
Line 75: Line 79:
=\frac{5}{6}
=\frac{5}{6}
</cmath>
</cmath>
<math>\frac{[CDEF]}{[CFB]}=\frac{\frac{5}{6}}{\frac{2}{3}}=\boxed{\textbf{(A) } 5:4}</math>
<imath>\frac{[CDEF]}{[CFB]}=\frac{\frac{5}{6}}{\frac{2}{3}}=\boxed{\textbf{(A) } 5:4}</imath>


==🎥✨ Video Solution by Scholars Foundation ➡️ (Easy-to-Understand 💡✔️)==
==🎥✨ Video Solution by Scholars Foundation ➡️ (Easy-to-Understand 💡✔️)==

Latest revision as of 20:25, 11 November 2025

Problem

Quadrilateral $ABCD$ is a parallelogram, and $E$ is the midpoint of the side $\overline{AD}$. Let $F$ be the intersection of lines $EB$ and $AC$. What is the ratio of the area of quadrilateral $CDEF$ to the area of $\triangle CFB$?

$\textbf{(A) } 5:4 \qquad\textbf{(B) } 4:3 \qquad\textbf{(C) } 3:2 \qquad\textbf{(D) } 5:3 \qquad\textbf{(E) } 2:1$

Solution 1

Let $AB = CD$ have length $b$ and let the altitude of the parallelogram perpendicular to $\overline{AD}$ have length $h$.

The area of the parallelogram is $bh$ and the area of $\triangle ABE$ equals $\frac{(b/2)(h)}{2} = \frac{bh}{4}$. Thus, the area of quadrilateral $BCDE$ is $bh - \frac{bh}{4} = \frac{3bh}{4}$.

We have from $AA$ that $\triangle CBF \sim \triangle AEF$. Also, $CB/AE = 2$, so the length of the altitude of $\triangle CBF$ from $F$ is twice that of $\triangle AEF$. This means that the altitude of $\triangle CBF$ is $2h/3$, so the area of $\triangle CBF$ is $\frac{(b)(2h/3)}{2} = \frac{bh}{3}$.

Then, the area of quadrilateral $CDEF$ equals the area of $BCDE$ minus that of $\triangle CBF$, which is $\frac{3bh}{4} - \frac{bh}{3} = \frac{5bh}{12}$. Finally, the ratio of the area of $CDEF$ to the area of triangle $CFB$ is $\frac{\frac{5bh}{12}}{\frac{bh}{3}} = \frac{\frac{5}{12}}{\frac{1}{3}} = \frac{5}{4}$, so the answer is $\boxed{\textbf{(A) } 5:4}$.

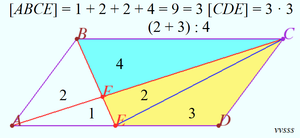
Solution 2

Let $[AFE]=1$. Since $\triangle AFE\sim\triangle CFB$ with a scale factor of $2$, $[CFB]=4$. The scale factor of $2$ also means that $\dfrac{AF}{FC}=\dfrac{1}{2}$, therefore since $\triangle BCF$ and $\triangle BFA$ have the same height, $[BFA]=2$. Since $ABCD$ is a parallelogram, \[[BCA]=[DAC]\implies4+2=1+[CDEF]\implies [CDEF]=5\implies\boxed{\text{(A) }5:4}\]

vladimir.shelomovskii@gmail.com, vvsss

Solution 3 (Techniques)

We assert that $ABCD$ is a square of side length $6$. Notice that $\triangle AFE\sim\triangle CFB$ with a scale factor of $2$. Since the area of $\triangle ABC$ is $18 \implies$ the area of $\triangle CFB$ is $12$, so the area of $\triangle AFE$ is $3$. Thus the area of $CDEF$ is $18-3=15$, and we conclude that the answer is $\frac{15}{12}\implies\boxed{\text{(A) }5:4}$ 

~Tacos_are_yummy_1

Solution 4

Let $ABCE$ be a square with side length $1$, to assist with calculations. We can put this on the coordinate plane with the points $D = (0,0)$, $C = (1, 0)$, $B = (1, 1)$, and $A = (0, 1)$. We have $E = (0, 0.5)$. Therefore, the line $EB$ has slope $0.5$ and y-intercept $0.5$. The equation of the line is then $y = 0.5x + 0.5$. The equation of line $AC$ is $y = -x + 1$. The intersection is when the lines are equal to each other, so we solve the equation. $0.5x + 0.5 = -x + 1$, so $x = \frac{1}{3}$. Therefore, plugging it into the equation, we get $y= \frac{2}{3}$. Using the shoelace theorem, we get the area of $CDEF$ to be $\frac{5}{12}$ and the area of $CFB$ to be $\frac{1}{3}$, so our ratio is $\frac{\frac{5}{12}}{\frac{1}{3}} = \boxed{(A) 5:4}$ ~idk12345678

Solution 5 (wlog)

Let $ABCE$ be a square with side length $2$. We see that $\triangle AFE \sim \triangle CFB$ by a Scale factor of $2$. Let the altitude of $\triangle AFE$ and altitude of $\triangle CFB$ be $h$ and $2h$, respectively. We know that $h+2h$ is equal to $2$, as the height of the square is $2$. Solving this equation, we get that $h = \frac{2}3.$ This means $[\triangle CFB] = \frac{4}3,$ we can also calculate the area of $\triangle ABE$. Adding the area we of $\triangle CFB$ and $\triangle ABE$ we get $\frac{7}3.$ We can then subtract this from the total area of the square: $4$, this gives us $\frac{5}3$ for the area of quadrilateral $CFED.$ Then we can compute the ratio which is equal to $\boxed{\textbf{(A) } 5:4}.$

~yuvag

(why does the $\LaTeX$ always look so bugged.)

Solution 6 (barycentrics)

$A=(1,0,0), B=(0,1,0), C=(0,0,1), D=(1,-1,1)$. Since $E$ is the midpoint of $\overline{AD}$, $E=(1,-0.5,0.5)$. The equation of $\overline{EB}$ is: \[0 = \begin{vmatrix} x & y & z \\ 1 & -0.5 & 0.5 \\ 0 & 1 & 0 \end{vmatrix}\] The equation of $\overline{AC}$ is: \[0 = \begin{vmatrix} x & y & z \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{vmatrix}\] We also know that $x+y+z=1$. To find the intersection, we can solve the system of equations. Solving, we get $x=2/3,y=0,z=1/3$. Therefore, $F=\left(\frac{2}{3}, 0, \frac{1}{3}\right)$. Using barycentric area formula, \[\frac{[CFB]}{[ABC]} = \begin{vmatrix} 0 & 0 & 1 \\ 2/3 & 0 & 1/3 \\ 0 & 1 & 0 \end{vmatrix} =\frac{2}{3}\] \[\frac{[CDEF]}{[ABC]} = \begin{vmatrix} 0 & 0 & 1 \\ 1 & -0.5 & 0.5 \\ 2/3 & 0 & 1/3 \end{vmatrix} + \begin{vmatrix} 0 & 0 & 1 \\ 1 & -1 & 1 \\ 1 & -0.5 & 0.5 \end{vmatrix} =\frac{5}{6}\] $\frac{[CDEF]}{[CFB]}=\frac{\frac{5}{6}}{\frac{2}{3}}=\boxed{\textbf{(A) } 5:4}$

🎥✨ Video Solution by Scholars Foundation ➡️ (Easy-to-Understand 💡✔️)

https://youtu.be/T_QESWAKUUk?si=TG7ToQnDsYKsNSSJ&t=648

Video Solution 1 by Pi Academy (Fast and Easy ⚡🚀)

https://youtu.be/QLziG_2e7CY?feature=shared

~ Pi Academy

Video Solution 2 by SpreadTheMathLove

https://www.youtube.com/watch?v=24EZaeAThuE

Video Solution 3 by TheBeautyofMath

https://youtu.be/ZaHv4UkXcbs?t=1360

~IceMatrix

See also

2024 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 9 		Followed by
Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America.

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2024_AMC_10B_Problems/Problem_10&oldid=268687"