Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2022 MPFG Problem19: Difference between revisions

← Older edit
Cassphe (talk | contribs)
editor
207 edits
Cassphe (talk | contribs)
editor
207 edits
 
(11 intermediate revisions by 2 users not shown)
Line 1: Line 1:
==Problem==
==Problem==
Let <math>S_-</math> be the semicircular arc defined by
Let <imath>S_-</imath> be the semicircular arc defined by
<cmath>(x+1)^2 + (y-\frac{3}{2})^2 = \frac{1}{4} and x \leq -1. </cmath>
<cmath>(x+1)^2 + (y-\frac{3}{2})^2 = \frac{1}{4} and x \leq -1. </cmath>
Let <math>S_+</math> be the semicircular arc defined by
Let <imath>S_+</imath> be the semicircular arc defined by
<cmath>(x-1)^2 + (y-\frac{3}{2})^2 = \frac{1}{4} and x \leq -1. </cmath>
<cmath>(x-1)^2 + (y-\frac{3}{2})^2 = \frac{1}{4} and x \leq -1. </cmath>


Let <math>R</math> be the locus of points <math>P</math> such that <math>P</math> is the intersection of two lines, one of the form <math>Ax + By = 1</math> where <math>(A,B) \in S_-</math> and the other of the form <math>Cx + Dy = 1</math> where <math>(C, D) \in S_+</math>. What is the area of <math>R</math>? Express your answer as a fraction in simplest form.
Let <imath>R</imath> be the locus of points <imath>P</imath> such that <imath>P</imath> is the intersection of two lines, one of the form <imath>Ax + By = 1</imath> where <imath>(A,B) \in S_-</imath> and the other of the form <imath>Cx + Dy = 1</imath> where <imath>(C, D) \in S_+</imath>. What is the area of <imath>R</imath>? Express your answer as a fraction in simplest form.


Because <math>Ax+By=1,Cx+Dy=1 ==> (A,B),(C,D)</math> is a solution set of <math>xX+yY=1</math>, which means that the <math>2</math> coordinates are on the line of <math>xX+yY=1</math>.
==Solution 1==


<math>xX+yY=1 ==> \frac{x}{\frac{1}{x}}+\frac{y}{\frac{1}{y}} = 1</math>
Because <imath>Ax+By=1,Cx+Dy=1 ==> (A,B),(C,D)</imath> is a solution set of <imath>xX+yY=1</imath>, which means that the <imath>2</imath> coordinates are on the line of <imath>xX+yY=1</imath>.


<math>S=\int_{x_0}^{x_1} y(x) \,dx</math>
<imath>xX+yY=1 ==> \frac{x}{\frac{1}{X}}+\frac{y}{\frac{1}{Y}} = 1</imath>


Let <math>m=\frac{1}{x}</math>.
<imath>S=\int_{x_0}^{x_1} y(x) \,dx</imath>


<math>\frac{1}{a} = \frac{m-1}{m} ==> a=\frac{m}{m-1} = \frac{\frac{1}{x}}{\frac{1}{x}-1} = \frac{1}{1-x} = \frac{1}{y_1}</math>
Let <imath>m=\frac{1}{x}</imath>.


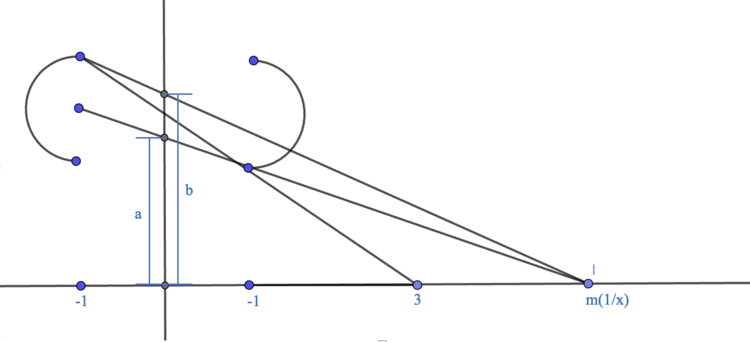
<math>\frac{b}{2} = \frac{m}{m+1} ==> b=\frac{2m}{m+1} = \frac{\frac{2}{x}}{\frac{1}{x}+1} = \frac{2}{1+x} = \frac{1}{y_1}</math>
[[File:2022mpfg19.png|750px|center]]


<math>\left| y_2=y_1 \right| ==> 1-x=\frac{1+x}{2}</math> <math>x_1=\frac{1}{3}</math>
<imath>\frac{1}{a} = \frac{m-1}{m} ==> a=\frac{m}{m-1} = \frac{\frac{1}{x}}{\frac{1}{x}-1} = \frac{1}{1-x} = \frac{1}{y_1}</imath>


<math>S = 2\int_{0}^\frac{1}{3} (-\frac{3}{2}x+\frac{1}{2}) \,dx</math>
<imath>\frac{b}{2} = \frac{m}{m+1} ==> b=\frac{2m}{m+1} = \frac{\frac{2}{x}}{\frac{1}{x}+1} = \frac{2}{1+x} = \frac{1}{y_2}</imath>


<math>=2(=\frac{3}{4}x^2+\frac{1}{2}x)</math>
<imath>\left| y_2 - y_1 \right| = (1-x) -(\frac{1+x}{2}) = (-\frac{3}{2}x+\frac{1}{2})</imath>
 
and m(<imath>\frac{1}{x}</imath>) ranging from 3 to infinite <imath>==></imath>  <imath>x_0=0</imath> , <imath>x_1=\frac{1}{3}</imath>
 
<imath>S = 2\int_{0}^\frac{1}{3} (-\frac{3}{2}x+\frac{1}{2}) \,dx</imath>        (times 2 because on both sides）
 
<imath>=\left. 2(\frac{3}{4}x^2+\frac{1}{2}x)\right|_{0}^{\frac{1}{3}} = 2(-\frac{1}{12} + \frac{1}{6}) = \boxed{\frac{1}{6}}</imath>
 
~cassphe

Latest revision as of 08:54, 7 November 2025

Problem

Let $S_-$ be the semicircular arc defined by \[(x+1)^2 + (y-\frac{3}{2})^2 = \frac{1}{4} and x \leq -1.\] Let $S_+$ be the semicircular arc defined by \[(x-1)^2 + (y-\frac{3}{2})^2 = \frac{1}{4} and x \leq -1.\]

Let $R$ be the locus of points $P$ such that $P$ is the intersection of two lines, one of the form $Ax + By = 1$ where $(A,B) \in S_-$ and the other of the form $Cx + Dy = 1$ where $(C, D) \in S_+$. What is the area of $R$? Express your answer as a fraction in simplest form.

Solution 1

Because $Ax+By=1,Cx+Dy=1 ==> (A,B),(C,D)$ is a solution set of $xX+yY=1$, which means that the $2$ coordinates are on the line of $xX+yY=1$.

$xX+yY=1 ==> \frac{x}{\frac{1}{X}}+\frac{y}{\frac{1}{Y}} = 1$

$S=\int_{x_0}^{x_1} y(x) \,dx$

Let $m=\frac{1}{x}$.

$\frac{1}{a} = \frac{m-1}{m} ==> a=\frac{m}{m-1} = \frac{\frac{1}{x}}{\frac{1}{x}-1} = \frac{1}{1-x} = \frac{1}{y_1}$

$\frac{b}{2} = \frac{m}{m+1} ==> b=\frac{2m}{m+1} = \frac{\frac{2}{x}}{\frac{1}{x}+1} = \frac{2}{1+x} = \frac{1}{y_2}$

$\left| y_2 - y_1 \right| = (1-x) -(\frac{1+x}{2}) = (-\frac{3}{2}x+\frac{1}{2})$

and m($\frac{1}{x}$) ranging from 3 to infinite $==>$ $x_0=0$ , $x_1=\frac{1}{3}$

$S = 2\int_{0}^\frac{1}{3} (-\frac{3}{2}x+\frac{1}{2}) \,dx$ (times 2 because on both sides）

$=\left. 2(\frac{3}{4}x^2+\frac{1}{2}x)\right|_{0}^{\frac{1}{3}} = 2(-\frac{1}{12} + \frac{1}{6}) = \boxed{\frac{1}{6}}$

~cassphe

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2022_MPFG_Problem19&oldid=266893"