Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2018 MPFG Problem 17: Difference between revisions

← Older edit
Cassphe (talk | contribs)
editor
207 edits
Cassphe (talk | contribs)
editor
207 edits
 
(2 intermediate revisions by the same user not shown)
Line 4: Line 4:
==Solution 1==
==Solution 1==


[[File:Mpfg201817.png|750px|center]]
[[File:Mpfg201817.png|600px|center]]


<math>Y</math>,<math>C</math> and <math>Z</math> is collinear.
<imath>Y</imath>,<imath>C</imath> and <imath>Z</imath> is collinear.


Because <math>\angle ACB = \angle AZB = 90^{\circ}</math>, <math>ACBZ</math> is concyclic. <math>\angle ZCB = \angle ZAB = 15^{\circ}</math>  
Because <imath>\angle ACB = \angle AZB = 90^{\circ}</imath>, <imath>ACBZ</imath> is concyclic. <imath>\angle ZCB = \angle ZAB = 15^{\circ}</imath>  


<math>\angle ZCX = 15^{\circ} + 75^{\circ} = 90^{\circ}</math>
<imath>\angle ZCX = 15^{\circ} + 75^{\circ} = 90^{\circ}</imath>


<math>S_{\Delta XYZ} = S_{ACBZ} = S_{\Delta ACB} + S_{\Delta AZB} = 6 + \frac{1}{2} \cdot 5^2 \cdot sin15^{\circ}cos15^{\circ} = 6 + \frac{1}{2} \cdot 5^2 \cdot \frac{1}{2}sin30^{\circ} = 6+\frac{25}{8} = \frac{73}{8}</math>
<imath>S_{\Delta XYZ} = S_{ACBZ} = S_{\Delta ACB} + S_{\Delta AZB} = 6 + \frac{1}{2} \cdot 5^2 \cdot sin15^{\circ}cos15^{\circ} = 6 + \frac{1}{2} \cdot 5^2 \cdot \frac{1}{2}sin30^{\circ} = 6+\frac{25}{8} = \boxed{\frac{73}{8}}</imath>
 
~cassphe

Latest revision as of 09:39, 7 November 2025

Problem

Let $ABC$ be a triangle with $AB = 5$, $BC = 4$, and $CA = 3$. On each side of $ABC$, externally erect a semicircle whose diameter is the corresponding side. Let $X$ be on the semicircular arc erected on side $BC$ such that $\angle CBX$ has measure $15^{\circ}$. Let $Y$ be on the semicircular arc erected on side $CA$ such that $\angle ACY$ has measure $15^{\circ}$. Similarly, let $Z$ be on the semicircular arc erected on side $AB$ such that $\angle BAZ$ has measure $15^{\circ}$. What is the area of triangle $\Delta XYZ$? Express your answer as a fraction in simplest form.

Solution 1

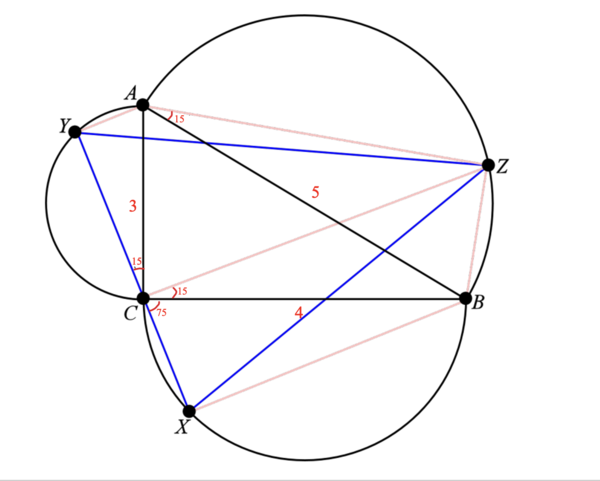
$Y$,$C$ and $Z$ is collinear.

Because $\angle ACB = \angle AZB = 90^{\circ}$, $ACBZ$ is concyclic. $\angle ZCB = \angle ZAB = 15^{\circ}$

$\angle ZCX = 15^{\circ} + 75^{\circ} = 90^{\circ}$

$S_{\Delta XYZ} = S_{ACBZ} = S_{\Delta ACB} + S_{\Delta AZB} = 6 + \frac{1}{2} \cdot 5^2 \cdot sin15^{\circ}cos15^{\circ} = 6 + \frac{1}{2} \cdot 5^2 \cdot \frac{1}{2}sin30^{\circ} = 6+\frac{25}{8} = \boxed{\frac{73}{8}}$

~cassphe

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2018_MPFG_Problem_17&oldid=266928"