2012 MPFG Problem 8: Difference between revisions
m →Notes |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 2: | Line 2: | ||
Suppose that <math>x</math>, <math>y</math>, and <math>z</math> are real numbers such that <math>x + y + z = 3</math> and <math>x^{2} + y^{2} + z^{2} = 6</math>. What is the largest possible value of <math>z</math>? Express your answer in the form <math>a +\sqrt{b}</math>, where <math>a</math> and <math>b</math> are positive integers. | Suppose that <math>x</math>, <math>y</math>, and <math>z</math> are real numbers such that <math>x + y + z = 3</math> and <math>x^{2} + y^{2} + z^{2} = 6</math>. What is the largest possible value of <math>z</math>? Express your answer in the form <math>a +\sqrt{b}</math>, where <math>a</math> and <math>b</math> are positive integers. | ||
== | ==Notes== | ||
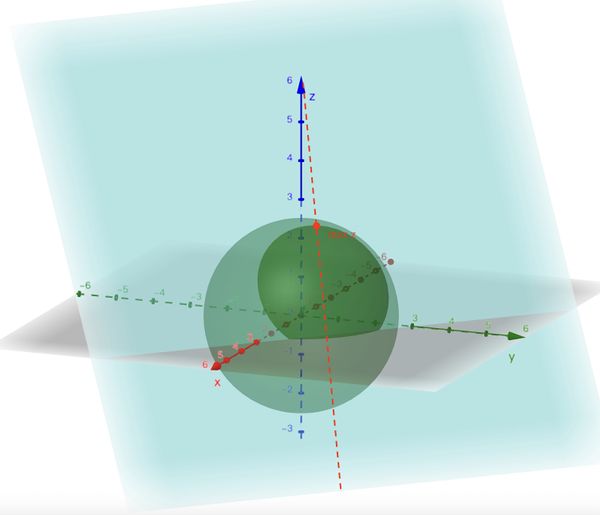
We can actually think of this question through its analytic geometric meaning/ As shown, the < | We can actually think of this question through its analytic geometric meaning/ As shown, the <imath>1st</imath> equation creates a plane made by connecting the points <imath>(3,0,0)</imath>, <imath>(0,3,0)</imath>, and <imath>(0,0,3)</imath>. The <imath>2nd</imath> equation creates a sphere with radius <imath>\sqrt{6}</imath> and a center at <imath>(0,0,0)</imath>. The intersections of the <imath>2</imath> equations create a circle. We want the maximum value of <imath>z</imath>, which is obviously located on the "axis of symmetry" of the graph. | ||
[[File:Hihihi.jpg|600px|center]] | [[File:Hihihi.jpg|600px|center]] | ||
~cassphe | |||
Latest revision as of 09:01, 7 November 2025
Problem
Suppose that 
, 
, and 
are real numbers such that 
and 
. What is the largest possible value of ? Express your answer in the form 
, where 
and 
are positive integers.
Notes
We can actually think of this question through its analytic geometric meaning/ As shown, the 
equation creates a plane made by connecting the points 
, 
, and 
. The 
equation creates a sphere with radius 
and a center at 
. The intersections of the 
equations create a circle. We want the maximum value of , which is obviously located on the "axis of symmetry" of the graph.
~cassphe
