Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2005 AMC 12A Problems/Problem 7: Difference between revisions

← Older edit
Wxl18 (talk | contribs)
editor
10 edits
Sevenoptimus (talk | contribs)
editor
698 edits
m Fixed problem statement
 
(2 intermediate revisions by 2 users not shown)
Line 1: Line 1:
== Problem ==
== Problem ==
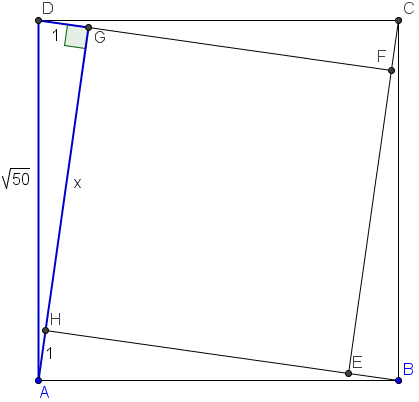
[[Square]] <math>EFGH</math> is inside the square <math>ABCD</math> so that each side of <math>EFGH</math> can be extended to pass through a vertex of <math>ABCD</math>. Square <math>ABCD</math> has side length <math>\sqrt {50}</math> and <math>BE = 1</math>. What is the area of the inner square <math>EFGH</math>?
Square <math>EFGH</math> is inside square <math>ABCD</math> so that each side of <math>EFGH</math> can be extended to pass through a vertex of <math>ABCD</math>. Square <math>ABCD</math> has side length <math>\sqrt{50}</math>, <math>E</math> is between <math>B</math> and <math>H</math>, and <math>BE = 1</math>. What is the area of the inner square <math>EFGH</math>?
 
<asy>
unitsize(4cm);
defaultpen(linewidth(.8pt)+fontsize(10pt));
pair D=(0,0), C=(1,0), B=(1,1), A=(0,1);
pair F=intersectionpoints(Circle(D,2/sqrt(5)),Circle(A,1))[0];
pair G=foot(A,D,F), H=foot(B,A,G), E=foot(C,B,H);
draw(A--B--C--D--cycle);
draw(D--F);
draw(C--E);
draw(B--H);
draw(A--G);
label("$A$",A,NW);
label("$B$",B,NE);
label("$C$",C,SE);
label("$D$",D,SW);
label("$E$",E,NNW);
label("$F$",F,ENE);
label("$G$",G,SSE);
label("$H$",H,WSW);
</asy>


<math>
<math>
(\mathrm {A}) \ 25 \qquad (\mathrm {B}) \ 32 \qquad (\mathrm {C})\ 36 \qquad (\mathrm {D}) \ 40 \qquad (\mathrm {E})\ 42
(\mathrm {A}) \ 25 \qquad (\mathrm {B}) \ 32 \qquad (\mathrm {C})\ 36 \qquad (\mathrm {D}) \ 40 \qquad (\mathrm {E})\ 42
</math>
</math>
== Solution ==
== Solution ==
[[Image:2005_12A_AMC-7b.png]]
[[Image:2005_12A_AMC-7b.png]]
Line 13: Line 35:


Notice the [[right triangle]] (in blue) with legs <math>1, x+1</math> and [[hypotenuse]] <math>\sqrt{50}</math>. By the [[Pythagorean Theorem]], we have <math>1^2 + (x+1)^2 = (\sqrt{50})^2 \Longrightarrow (x+1)^2 = 49 \Longrightarrow x = 6</math>. Thus, <math>[EFGH] = x^2 = 36\ \mathrm{(C)}</math>
Notice the [[right triangle]] (in blue) with legs <math>1, x+1</math> and [[hypotenuse]] <math>\sqrt{50}</math>. By the [[Pythagorean Theorem]], we have <math>1^2 + (x+1)^2 = (\sqrt{50})^2 \Longrightarrow (x+1)^2 = 49 \Longrightarrow x = 6</math>. Thus, <math>[EFGH] = x^2 = 36\ \mathrm{(C)}</math>
== Solution 2 ==
You can also notice that the four triangles <math>\triangle ABH,\triangle BCE,\triangle CDF,\triangle DAG</math> are congruent because the right angles of square <math>ABCD</math> cause them to be similar, and the hypotenuse of the triangles are the same because they are the sides of the square. Then you have <cmath>[ABCD]-4*7=50-28=22\Rightarrow\boxed{C}.</cmath>
Solution by wxl18
== See also ==
== See also ==
{{AMC12 box|year=2005|num-b=6|num-a=8|ab=A}}
{{AMC12 box|year=2005|num-b=6|num-a=8|ab=A}}

Latest revision as of 13:48, 1 July 2025

Problem

Square $EFGH$ is inside square $ABCD$ so that each side of $EFGH$ can be extended to pass through a vertex of $ABCD$. Square $ABCD$ has side length $\sqrt{50}$, $E$ is between $B$ and $H$, and $BE = 1$. What is the area of the inner square $EFGH$?

[asy] unitsize(4cm); defaultpen(linewidth(.8pt)+fontsize(10pt)); pair D=(0,0), C=(1,0), B=(1,1), A=(0,1); pair F=intersectionpoints(Circle(D,2/sqrt(5)),Circle(A,1))[0]; pair G=foot(A,D,F), H=foot(B,A,G), E=foot(C,B,H); draw(A--B--C--D--cycle); draw(D--F); draw(C--E); draw(B--H); draw(A--G); label("$A$",A,NW); label("$B$",B,NE); label("$C$",C,SE); label("$D$",D,SW); label("$E$",E,NNW); label("$F$",F,ENE); label("$G$",G,SSE); label("$H$",H,WSW); [/asy]

$(\mathrm {A}) \ 25 \qquad (\mathrm {B}) \ 32 \qquad (\mathrm {C})\ 36 \qquad (\mathrm {D}) \ 40 \qquad (\mathrm {E})\ 42$

Solution

Arguable the hardest part of this question is to visualize the diagram. Since each side of $EFGH$ can be extended to pass through a vertex of $ABCD$, we realize that $EFGH$ must be tilted in such a fashion. Let a side of $EFGH$ be $x$.

Notice the right triangle (in blue) with legs $1, x+1$ and hypotenuse $\sqrt{50}$. By the Pythagorean Theorem, we have $1^2 + (x+1)^2 = (\sqrt{50})^2 \Longrightarrow (x+1)^2 = 49 \Longrightarrow x = 6$. Thus, $[EFGH] = x^2 = 36\ \mathrm{(C)}$

See also

2005 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 6 		Followed by
Problem 8
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

These problems are copyrighted © by the Mathematical Association of America.

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2005_AMC_12A_Problems/Problem_7&oldid=253018"