2019 AIME II Problems/Problem 15: Difference between revisions
mNo edit summary |
|||
| (52 intermediate revisions by 16 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
In acute triangle <math>ABC</math> points <math>P</math> and <math>Q</math> are the feet of the perpendiculars from <math>C</math> to <math>\overline{AB}</math> and from <math>B</math> to <math>\overline{AC}</math>, respectively. Line <math>PQ</math> intersects the circumcircle of <math>\triangle ABC</math> in two distinct points, <math>X</math> and <math>Y</math>. Suppose <math>XP=10</math>, <math>PQ=25</math>, and <math>QY=15</math>. The value of <math>AB\cdot AC</math> can be written in the form <math>m\sqrt n</math> where <math>m</math> and <math>n</math> are positive | In acute triangle <math>ABC</math> points <math>P</math> and <math>Q</math> are the feet of the perpendiculars from <math>C</math> to <math>\overline{AB}</math> and from <math>B</math> to <math>\overline{AC}</math>, respectively. Line <math>PQ</math> intersects the circumcircle of <math>\triangle ABC</math> in two distinct points, <math>X</math> and <math>Y</math>. Suppose <math>XP=10</math>, <math>PQ=25</math>, and <math>QY=15</math>. The value of <math>AB\cdot AC</math> can be written in the form <math>m\sqrt n</math> where <math>m</math> and <math>n</math> are positive integers, and <math>n</math> is not divisible by the square of any prime. Find <math>m+n</math>. | ||
== | ==Diagram== | ||
<asy> | |||
size(200); | |||
defaultpen(linewidth(0.4)+fontsize(10)); | |||
pen s = linewidth(0.8)+fontsize(8); | |||
pair A,B,C,P,Q,X,Y,O; | |||
O = origin; | |||
real theta = 32; | |||
A = dir(180+theta); | |||
B = dir(-theta); | |||
C = dir(75); | |||
Q = foot(B,A,C); | |||
P = foot(C,A,B); | |||
path c = circumcircle(A,B,C); | |||
X = IP(c, Q--(2*P-Q)); | |||
Y = IP(c, P--(2*Q-P)); | |||
draw(A--B--C--A, black+0.8); | |||
draw(c^^X--Y^^B--Q^^C--P); | |||
dot("$A$", A, SW); | |||
dot("$B$", B, SE); | |||
dot("$C$", C, N); | |||
dot("$P$", P, SW); | |||
dot("$Q$", Q, W); | |||
dot("$X$", X, SE); | |||
dot("$Y$", Y, NW); | |||
label("$25$", P--Q, SW); | |||
label("$15$", Q--Y, SW); | |||
label("$10$", X--P, SW); | |||
</asy> | |||
==Solution 1== | |||
First we have <math>a\cos A=PQ=25</math>, and <math>(a\cos A)(c\cos C)=(a\cos C)(c\cos A)=AP\cdot PB=10(25+15)=400</math> by PoP. Similarly, <math>(a\cos A)(b\cos B)=15(10+25)=525,</math> and dividing these each by <math>a\cos A</math> gives | |||
</math> | <math>b\cos B=21,c\cos C=16</math>. | ||
It is known that the sides of the orthic triangle are <math>a\cos A,b\cos B,c\cos C</math>, and its angles are <math>\pi-2A</math>,<math>\pi-2B</math>, and <math>\pi-2C</math>. We thus have the three sides of the orthic triangle now. | |||
Letting <math>D</math> be the foot of the altitude from <math>A</math>, we have, in <math>\triangle DPQ</math>, | |||
<cmath>\cos P,\cos Q=\frac{21^2+25^2-16^2}{2\cdot 21\cdot 25},\frac{16^2+25^2-21^2}{2\cdot 16\cdot 25}= \frac{27}{35}, \frac{11}{20}.</cmath> | |||
<cmath>\Rightarrow \cos B=\cos\left(\tfrac 12 (\pi-P)\right)=\sin\tfrac 12 P =\sqrt{\frac{4}{35}},</cmath> | |||
similarly, we get | |||
<cmath>\cos C=\cos\left(\tfrac 12 (\pi-Q)\right)=\sin\tfrac 12 Q=\sqrt{\frac{9}{40}}.</cmath> | |||
To finish, <cmath>bc= \frac{(b\cos B)(c\cos C)}{\cos B\cos C}=\frac{16\cdot 21}{(2/\sqrt{35})(3/\sqrt{40})}=560\sqrt{14}.</cmath> | |||
The requested sum is <math>\boxed{574}</math>. | |||
- crazyeyemoody907 | |||
Remark: The proof that <math>a \cos A = PQ</math> can be found here: http://www.irmo.ie/5.Orthic_triangle.pdf | |||
==Solution 2== | |||
</math> | Let <math>BC=a</math>, <math>AC=b</math>, and <math>AB=c</math>. Let <math>\cos\angle A=k</math>. Then <math>AP=bk</math> and <math>AQ=ck</math>. | ||
By Power of a Point theorem, | |||
<cmath>\begin{align} | |||
AP\cdot BP=XP\cdot YP \quad &\Longrightarrow \quad b^2k^2-bck+400=0\\ | |||
AQ\cdot CQ=YQ\cdot XQ \quad &\Longrightarrow \quad c^2k^2-bck+525=0 | |||
\end{align}</cmath> | |||
Thus <math>bck = (bk)^2+400=(ck)^2+525 = u</math>. Then <math>bk=\sqrt{u-400}</math>, <math>ck=\sqrt{u-525}</math>, and | |||
<cmath>k=\sqrt{\frac{(u-400)(u-525)}{u^2}}</cmath> | |||
Use the Law of Cosines in <math>\triangle APQ</math> to get <math>25^2=b^2k^2+c^2k^2-2bck^3 = 2bck-925-2bck^3</math>, which rearranges to <cmath>775=bck - k^2\cdot bck = u-\frac{(u-400)(u-525)}{u}</cmath>Upon simplification, this reduces to a linear equation in <math>u</math>, with solution <math>u=1400</math>. Then <cmath>AB\cdot AC = bc = \frac 1{k}\cdot bck = \frac{u^2}{\sqrt{(u-400)(u-525)}}=560 \sqrt{14}</cmath> | |||
So the final answer is <math>560 + 14 = \boxed{574}</math> | |||
By SpecialBeing2017 | |||
==Solution 3== | |||
</math> \frac{ | Let <math>AP=p</math>, <math>PB=q</math>, <math>AQ=r</math>, and <math>QC=s</math>. By Power of a Point, | ||
<cmath>\begin{align} | |||
AP\cdot PB=XP\cdot YP \quad &\Longrightarrow \quad pq=400\\ | |||
AQ\cdot QC=YQ\cdot XQ \quad &\Longrightarrow \quad rs=525 | |||
\end{align}</cmath> | |||
Points <math>P</math> and <math>Q</math> lie on the circle, <math>\omega</math>, with diameter <math>BC</math>, and pow<math>(A,\omega) = AP\cdot AB = AQ\cdot AC</math>, so <cmath> p(p+q)=r(r+s)\quad \Longrightarrow \quad p^2-r^2=125</cmath> Use Law of Cosines in <math>\triangle APQ</math> to get <math>25^2=p^2+r^2-2pr\cos A</math>; since <math>\cos A = \frac r{p+q}</math>, this simplifies as | |||
<cmath>500 \ =\ 2r^2-\frac{2pr^2}{p+q} \ =\ 2r^2-\frac{2p^2r^2}{p^2+400} \ =\ \frac{800r^2}{r^2+525}</cmath> | |||
We get <math>r=5\sqrt{35}</math> and thus | |||
<cmath>r=5\sqrt{35}, \quad p = \sqrt{r^2+125} = 10\sqrt{10}, \quad q = \frac{400}{p} =4\sqrt{10}, \quad s= \frac{525}{r} = 3\sqrt{35}.</cmath> | |||
Therefore <math>AB\cdot AC = (p+q)\cdot(r+s) = 560\sqrt{14}</math>. So the answer is <math>560 + 14 = \boxed{574}</math> | |||
By asr41 | |||
==Solution 4 (Clean)== | |||
This solution is directly based of @CantonMathGuy's solution. | |||
We start off with a key claim. | |||
<i> Claim. </i> <math>XB \parallel AC</math> and <math>YC \parallel AB</math>. | |||
<i> Proof. </i> | |||
[[File:AIME-II-2019-15.png|350px|right]] | |||
Let <math>E</math> and <math>F</math> denote the reflections of the orthocenter over points <math>P</math> and <math>Q</math>, respectively. Since <math>EF \parallel XY</math> and <cmath>EF = 2 PQ = XP + PQ + QY = XY,</cmath> we have that <math>E X Y F</math> is a rectangle. Then, since <math>\angle XYF = 90^\circ</math> we obtain <math>\angle XBF = 90^\circ</math> (which directly follows from <math>XBYF</math> being cyclic); hence <math>\angle XBQ = \angle AQB</math>, or <math>XB \parallel AQ \Rightarrow XB \parallel AC</math>. | |||
Similarly, we can obtain <math>YC \parallel AB</math>. <math>\ \blacksquare</math> | |||
< | A direct result of this claim is that <math>\triangle BPX \sim \triangle APQ \sim \triangle CYQ</math>. | ||
Thus, we can set <math>AP = 5k</math> and <math>BP = 2k</math>, then applying Power of a Point on <math>P</math> we get <math>10 \cdot 40 = 10k^2 \implies k = 2\sqrt{10} \implies AB = 14 \sqrt{10}</math>. Also, we can set <math>AQ = 5l</math> and <math>CQ = 3l</math> and once again applying Power of a Point (but this time to <math>Q</math>) we get | |||
<math>\phantom{...................}15 \cdot 35 = 15l^2 \implies l = \sqrt{35} \implies AC = 8 \sqrt{35}</math>. | |||
Hence, | |||
<math>\phantom{...................}AB \cdot AC = 112 \sqrt{350} = 112 \cdot 5 \sqrt{14} = 560 \sqrt{14}</math> | |||
and the answer is <math>560 + 14 = \boxed{574}</math>. ~rocketsri | |||
==Solution 5== | |||
[[File:2019AIMEIIP15Solution.png|900px]] | |||
'''mathboy282''' | |||
== Video Solution == | |||
[https://youtu.be/gffk44T4MjM?si=gcSViECYKW982z1J 2019 AIME II #15] | |||
[https://mathproblemsolvingskills.wordpress.com/ MathProblemSolvingSkills.com] | |||
==Video Solution by MOP 2024== | |||
https://youtu.be/aYV09qIwTqs | |||
~r00tsOfUnity | |||
==Video Solution by Mr. Math== | |||
https://www.youtube.com/watch?v=rpNnK5n0_P0 | |||
==See Also== | ==See Also== | ||
{{AIME box|year=2019|n=II|num-b=14|after=Last Question}} | {{AIME box|year=2019|n=II|num-b=14|after=Last Question}} | ||
[[Category: Intermediate Geometry Problems]] | |||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 16:17, 21 October 2025
Problem
In acute triangle ![]() points
points ![]() and
and ![]() are the feet of the perpendiculars from
are the feet of the perpendiculars from ![]() to
to ![]() and from
and from ![]() to
to ![]() , respectively. Line
, respectively. Line ![]() intersects the circumcircle of
intersects the circumcircle of ![]() in two distinct points,
in two distinct points, ![]() and
and ![]() . Suppose
. Suppose ![]() ,
, ![]() , and
, and ![]() . The value of
. The value of ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
Diagram
![[asy] size(200); defaultpen(linewidth(0.4)+fontsize(10)); pen s = linewidth(0.8)+fontsize(8); pair A,B,C,P,Q,X,Y,O; O = origin; real theta = 32; A = dir(180+theta); B = dir(-theta); C = dir(75); Q = foot(B,A,C); P = foot(C,A,B); path c = circumcircle(A,B,C); X = IP(c, Q--(2*P-Q)); Y = IP(c, P--(2*Q-P)); draw(A--B--C--A, black+0.8); draw(c^^X--Y^^B--Q^^C--P); dot("$A$", A, SW); dot("$B$", B, SE); dot("$C$", C, N); dot("$P$", P, SW); dot("$Q$", Q, W); dot("$X$", X, SE); dot("$Y$", Y, NW); label("$25$", P--Q, SW); label("$15$", Q--Y, SW); label("$10$", X--P, SW); [/asy]](http://latex.artofproblemsolving.com/0/b/9/0b96efb71a1d1aef4a0c2f0c402c8d9d0e29cee0.png)
Solution 1
First we have ![]() , and
, and ![]() by PoP. Similarly,
by PoP. Similarly, ![]() and dividing these each by
and dividing these each by ![]() gives
gives
![]() .
.
It is known that the sides of the orthic triangle are ![]() , and its angles are
, and its angles are ![]() ,
,![]() , and
, and ![]() . We thus have the three sides of the orthic triangle now.
Letting
. We thus have the three sides of the orthic triangle now.
Letting ![]() be the foot of the altitude from
be the foot of the altitude from ![]() , we have, in
, we have, in ![]() ,
,
![]()
![]() similarly, we get
similarly, we get
![]() To finish,
To finish, ![]() The requested sum is
The requested sum is ![]() .
- crazyeyemoody907
.
- crazyeyemoody907
Remark: The proof that ![]() can be found here: http://www.irmo.ie/5.Orthic_triangle.pdf
can be found here: http://www.irmo.ie/5.Orthic_triangle.pdf
Solution 2
Let ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() . Then
. Then ![]() and
and ![]() .
.
By Power of a Point theorem,
![]() Thus
Thus ![]() . Then
. Then ![]() ,
, ![]() , and
, and
![]() Use the Law of Cosines in
Use the Law of Cosines in ![]() to get
to get ![]() , which rearranges to
, which rearranges to ![]() Upon simplification, this reduces to a linear equation in
Upon simplification, this reduces to a linear equation in ![]() , with solution
, with solution ![]() . Then
. Then ![]() So the final answer is
So the final answer is ![]()
By SpecialBeing2017
Solution 3
Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . By Power of a Point,
. By Power of a Point,
![]() Points
Points ![]() and
and ![]() lie on the circle,
lie on the circle, ![]() , with diameter
, with diameter ![]() , and pow
, and pow![]() , so
, so ![]() Use Law of Cosines in
Use Law of Cosines in ![]() to get
to get ![]() ; since
; since ![]() , this simplifies as
, this simplifies as
![]() We get
We get ![]() and thus
and thus
![]() Therefore
Therefore ![]() . So the answer is
. So the answer is ![]()
By asr41
Solution 4 (Clean)
This solution is directly based of @CantonMathGuy's solution. We start off with a key claim.
Claim. ![]() and
and ![]() .
.
Proof.
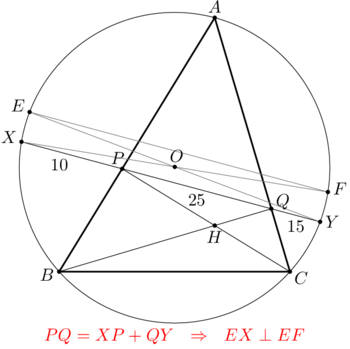
Let ![]() and
and ![]() denote the reflections of the orthocenter over points
denote the reflections of the orthocenter over points ![]() and
and ![]() , respectively. Since
, respectively. Since ![]() and
and ![]() we have that
we have that ![]() is a rectangle. Then, since
is a rectangle. Then, since ![]() we obtain
we obtain ![]() (which directly follows from
(which directly follows from ![]() being cyclic); hence
being cyclic); hence ![]() , or
, or ![]() .
.
Similarly, we can obtain ![]() .
. ![]()
A direct result of this claim is that ![]() .
.
Thus, we can set ![]() and
and ![]() , then applying Power of a Point on
, then applying Power of a Point on ![]() we get
we get ![]() . Also, we can set
. Also, we can set ![]() and
and ![]() and once again applying Power of a Point (but this time to
and once again applying Power of a Point (but this time to ![]() ) we get
) we get
![]() .
.
Hence,
![]()
and the answer is ![]() . ~rocketsri
. ~rocketsri
Solution 5
Video Solution
Video Solution by MOP 2024
~r00tsOfUnity
Video Solution by Mr. Math
https://www.youtube.com/watch?v=rpNnK5n0_P0
See Also
| 2019 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America. 










