2012 MPFG Problem 10: Difference between revisions
No edit summary |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
==Solution 1== | ==Solution 1== | ||
The question doesn't give us which angle of < | The question doesn't give us which angle of <imath>\Delta DFG</imath> is the right angle, so we would have to discuss different cases. Obviously <imath>\angle DFG</imath> can't be the right angle. | ||
<imath>\#1</imath> <imath>\angle FGD = 90^\circ</imath> | |||
[[File:DGF.png|200px|center]] | |||
Connect BE. We discover that DG and FD are consecutively the midlines of < | Connect BE. We discover that DG and FD are consecutively the midlines of <imath>\Delta BEC</imath> and <imath>\Delta ABC</imath>. | ||
< | <imath>AE = EC = BE = \frac{1}{2} AC</imath> | ||
< | <imath>GD = \frac{1}{2}BE = \frac{1}{2}EC</imath> | ||
< | <imath>FD = \frac{1}{2}AC = EC</imath> | ||
This gives us < | This gives us <imath>FD = 2GD</imath>, which means <imath>\Delta FDG</imath> is a <imath>30^\circ - 60^\circ - 90^\circ</imath> triangle. | ||
< | <imath>\angle CGD = \angle GDF = 60^\circ</imath>. Because <imath>DG = GC = \frac{1}{2} EC</imath>, <imath>\angle C = \frac{180^\circ-60^\circ}{2} = 60^\circ</imath> | ||
< | <imath>\Delta ABC</imath> is also a <imath>30^\circ - 60^\circ - 90^\circ</imath> triangle. | ||
< | <imath>\frac{BC}{AG} = \frac{1}{2\cdot\frac{3}{4}} = \frac{2}{3}</imath> | ||
< | <imath>\#2</imath> <imath>\angle FDG = 90^\circ</imath> | ||
[[File:FDG.png|250px|center]] | |||
< | Because <imath>\angle DGC = \angle FDG = 90^\circ</imath>, <imath>\angle C = \frac{180^\circ-90^\circ}{2} = 45^\circ</imath> | ||
< | <imath>\Delta ABC</imath> is a <imath>45^\circ - 45^\circ - 90^\circ</imath> triangle. | ||
The least possible value of < | <imath>\frac{BC}{AG} = \frac{1}{\sqrt{2}\cdot\frac{3}{4}} = \frac{2\sqrt{2}}{3}</imath> | ||
The least possible value of <imath>\frac{BC}{AG}</imath> is <imath>\boxed{\frac{2}{3}}</imath>. | |||
~cassphe | |||
Latest revision as of 09:38, 7 November 2025
Problem
Let ![]() be a triangle with a right angle
be a triangle with a right angle ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() , let
, let ![]() be the midpoint of
be the midpoint of ![]() , and let
, and let ![]() be the midpoint of
be the midpoint of ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() . One of the angles of
. One of the angles of ![]() is a right angle. What is the least possible value of
is a right angle. What is the least possible value of ![]() ? Express your answer as a fraction in simplest form.
? Express your answer as a fraction in simplest form.
Solution 1
The question doesn't give us which angle of ![]() is the right angle, so we would have to discuss different cases. Obviously
is the right angle, so we would have to discuss different cases. Obviously ![]() can't be the right angle.
can't be the right angle.
![]()
![]()
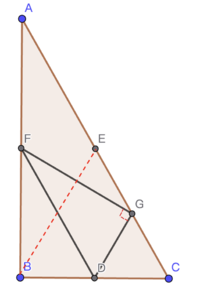
Connect BE. We discover that DG and FD are consecutively the midlines of ![]() and
and ![]() .
.
![]()
![]()
![]()
This gives us ![]() , which means
, which means ![]() is a
is a ![]() triangle.
triangle.
![]() . Because
. Because ![]() ,
, ![]()
![]() is also a
is also a ![]() triangle.
triangle.
![]()
![]()
![]()
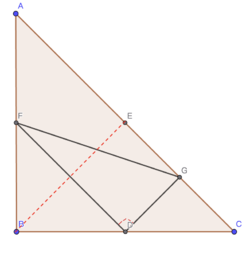
Because ![]() ,
, ![]()
![]() is a
is a ![]() triangle.
triangle.

The least possible value of ![]() is
is ![]() .
.
~cassphe









