Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2019 MPFG Problem 15: Difference between revisions

Aoum (talk | contribs)
editor
4,956 edits
Created page with "==Problem== How many ordered pairs <math>(x, y)</math> of real numbers <math>x</math> and <math>y</math> are there such that <math>-100 \pi \leq x \leq 100 \pi</math>, <math>-..."
 
Cassphe (talk | contribs)
editor
207 edits
 
Line 3: Line 3:


==Solution 1==
==Solution 1==
According to the <math>\tan</math> angle sum trigonometric identity,  
According to the <imath>\tan</imath> angle sum trigonometric identity,  


<cmath>
<cmath>
Line 17: Line 17:
</cmath>
</cmath>


The two equations <math>\tan x \cdot \tan y = \frac{20.19}{\tan 20.19} - 1</math> and <math>\tan x + \tan y = 20.19</math> create a set of [[Vieta's Formulas|Vieta's formulas]] for  
The two equations <imath>\tan x \cdot \tan y = \frac{20.19}{\tan 20.19} - 1</imath> and <imath>\tan x + \tan y = 20.19</imath> create a set of [[Vieta's Formulas|Vieta's formulas]] for  


<cmath>
<cmath>
Line 23: Line 23:
</cmath>
</cmath>


whose discriminant <math>\Delta</math> is obviously greater than 0. This indicates that there must be a constant value for the set <math>(\tan x, \tan y)</math>.
whose discriminant <imath>\Delta</imath> is obviously greater than 0. This indicates that there must be a constant value for the set <imath>(\tan x, \tan y)</imath>.


Assume that <math>\tan x > \tan y</math>. <math>\tan x</math> is represented by the upper blue line, <math>\tan y</math> is represented by the lower red line.
Assume that <imath>\tan x > \tan y</imath>. <imath>\tan x</imath> is represented by the upper blue line, <imath>\tan y</imath> is represented by the lower red line.


[[File:Forgot_line.png|710px|center]]
[[File:Forgot_line.png|710px|center]]


As we can see, each value of <math>x</math> matches a value of <math>y</math> on the other side of the <math>y</math>-axis. Because <math>x + y = 20.19</math>, which is approximately <math>6.42 \pi</math>, 6 values of <math>x/y</math> close to <math>-100 \pi</math> cannot be taken.
As we can see, each value of <imath>x</imath> matches a value of <imath>y</imath> on the other side of the <imath>y</imath>-axis. Because <imath>x + y = 20.19</imath>, which is approximately <imath>6.42 \pi</imath>, 6 values of <imath>x/y</imath> close to <imath>-100 \pi</imath> cannot be taken.


There are <math>200 - 6 = 194</math> values of <math>(x, y)</math> when <math>\tan x > \tan y</math>. Doubling this number, we get <math>\boxed{388}</math>.
There are <imath>200 - 6 = 194</imath> values of <imath>(x, y)</imath> when <imath>\tan x > \tan y</imath>. Doubling this number, we get <imath>\boxed{388}</imath>.


~cassphe
~cassphe


~edited by aoum
~edited by aoum

Latest revision as of 08:58, 7 November 2025

Problem

How many ordered pairs $(x, y)$ of real numbers $x$ and $y$ are there such that $-100 \pi \leq x \leq 100 \pi$, $-100 \pi \leq y \leq 100 \pi$, $x + y = 20.19$, and $\tan x + \tan y = 20.19$?

Solution 1

According to the $\tan$ angle sum trigonometric identity,

\[\tan(x + y) = \frac{\tan x + \tan y}{1 + \tan x \cdot \tan y}\]

\[\tan 20.19 = \frac{20.19}{1 + \tan x \cdot \tan y}\]

\[\tan x \cdot \tan y = \frac{20.19}{\tan 20.19} - 1\]

The two equations $\tan x \cdot \tan y = \frac{20.19}{\tan 20.19} - 1$ and $\tan x + \tan y = 20.19$ create a set of Vieta's formulas for

\[x^2 - 20.19x + \left( \frac{20.19}{\tan 20.19} - 1 \right) = 0,\]

whose discriminant $\Delta$ is obviously greater than 0. This indicates that there must be a constant value for the set $(\tan x, \tan y)$.

Assume that $\tan x > \tan y$. $\tan x$ is represented by the upper blue line, $\tan y$ is represented by the lower red line.

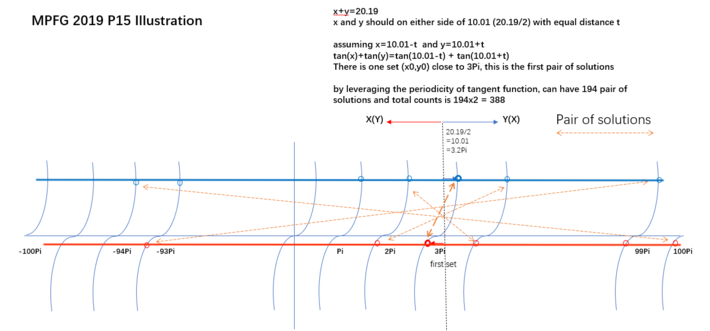
As we can see, each value of $x$ matches a value of $y$ on the other side of the $y$-axis. Because $x + y = 20.19$, which is approximately $6.42 \pi$, 6 values of $x/y$ close to $-100 \pi$ cannot be taken.

There are $200 - 6 = 194$ values of $(x, y)$ when $\tan x > \tan y$. Doubling this number, we get $\boxed{388}$.

~cassphe

~edited by aoum

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2019_MPFG_Problem_15&oldid=266897"