1966 IMO Problems/Problem 3: Difference between revisions

Latest revision as of 19:16, 10 November 2024

Problem

Prove that the sum of the distances of the vertices of a regular tetrahedron from the center of its circumscribed sphere is less than the sum of the distances of these vertices from any other point in space.

Solution

We will need the following lemma to solve this problem:

$\emph{Lemma:}$ Let $MNOP$ be a regular tetrahedron, and $T$ a point inside it. Let $x_1, x_2, x_3, x_4$ be the distances from $T$ to the faces $MNO, MNP, MOP$ , and $NOP$ . Then, $x_1 + x_2 + x_3 + x_4$ is constant, independent of $T$ .

$\emph{Proof:}$

We will compute the volume of $MNOP$ in terms of the areas of the faces and the distances from the point $T$ to the faces:

$\textrm{Volume}(MNOP) = [MNO] \cdot x_1 \cdot \frac{1}{3} + [MNP] \cdot x_2 \cdot \frac{1}{3} + [MOP] \cdot x_3 \cdot \frac{1}{3} + [NOP] \cdot x_4 \cdot \frac{1}{3}$ $= [MNO] \cdot \frac{(x_1 + x_2 + x_3 + x_4)}{3}$

because the areas of the four triangles are equal. ( $[ABC]$ stands for the area of $\triangle ABC$ .) Then

$\frac{3\cdot\textrm{Volume}(MNOP)}{[MNO]} = x_1 + x_2 + x_3 + x_4.$

This value is constant, so the proof of the lemma is complete.

$\emph{Proof of problem statement:}$

Let our tetrahedron be $ABCD$ , and the center of its circumscribed sphere be $O$ . Construct a new regular tetrahedron, $WXYZ$ , such that the centers of the faces of this tetrahedron are at $A$ , $B$ , $C$ , and $D$ .

For any point $P$ in $ABCD$ ,

$OA + OB + OC + OD = \sum \textrm{Distances from }O\textrm{ to faces of }WXYZ$ $= \sum \textrm{Distances from }P\textrm{ to faces of }WXYZ \leq PA + PB + PC + PD,$

with equality only occurring when $AP$ , $BP$ , $CP$ , and $DP$ are perpendicular to the faces of $WXYZ$ , meaning that $P = O$ . This completes the proof. $\square$

~mathboy100

Remarks (added by pf02, September 2024)

1. The text of the Lemma needed a little improvement, which I did.

2. The Solution above is not complete. It considered only points $P$ inside the tetrahedron, but the problem specifically said "any other point in space".

3. I will give another solution below, in which I will also fill in the gap of the solution above, mentioned in the preceding paragraph.

Solution 2

We will first prove the problem in the 2-dimensional case. We do this to convey the idea of the proof, and because we will use this in one spot in proving the 3-dimensional case. So let us prove that:

The sum of the distances of the vertices of an equilateral triangle $\triangle ABC$ from the center $O$ of its circumscribed circle is less than the sum of the distances of these vertices from any other point $P$ in the plane.

We will do the proof in three steps:

$\mathbf{1.}$ We will show that if $P$ is in one of the exterior regions, then there is a point $P_1$ on the boundary of the triangle (a vertex, or on a side), such that $PA + PB + PC > P_1A + P_1B + P_1C$ .

$\mathbf{2.}$ Then we will show that if $P$ is on the boundary, then $PA + PB + PC > OA + OB + OC$ .

$\mathbf{3.}$ For the final step, we will show that if $P$ is a point of minimum for $PA + PB + PC$ inside the triangle, then the extensions of $PA, PB, PC$ are perpendicular to the opposite sides $BC, AC, AB$ . This implies that $P = O$ .

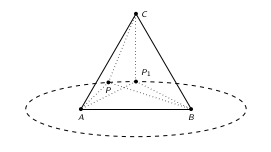
$\mathbf{Proof\ of\ 1:}$ If the point $P$ is outside the triangle, it can be in one of six regions as seen in the pictures below.

If $P$ is in a region delimited by extensions of two sides of the triangle, as in the picture on the left, we notice that by taking $P_1 = A$ , $PA + PB + PC > P_1A + P_1B + P_1C$ (because $P_1A = 0$ and $P_1B < PB$ as sides in an obtuse triangles, and similarly $P_1C < PC$ ).

If $P$ is in a region delimited by a segment which is a side of the triangle and by the extensions of two sides, as in the picture on the right, take $P_1 =$ the foot of the perpendicular from $P$ to $AB$ . Then $PA + PB + PC > P_1A + P_1B + P_1C$ (because the triangle $\triangle PP_1C$ is obtuse, and because the triangles $\triangle PP_1A, \triangle PP_1B$ are right triangles).

$\mathbf{Proof\ of\ 2:}$ Now assume that $P_1 = A$ . A direct, simple computation shows that $P_1A + P_1B + P_1C > OA + OB + OC$ (indeed, if we take the side of the triangle to be $1$ , then $P_1A + P_1B + P_1C = 2$ , and $OA + OB + OC = 3 \cdot \frac{\sqrt{3}}{3} = \sqrt{3}$ ).

Now assume that $P_1$ is on $AB$ . If $P_1$ is not the midpoint of $AB$ , let $P_2$ be the midpoint. Then $P_1A + P_1B + P_1C > P_2A + P_2B + P_2C$ (because $P_1A + P_1B = P_2A + P_2B = AB$ and $P_1C > P_2C$ ). A direct, simple computation shows that $P_2A + P_2B + P_2C > OA + OB + OC$ (indeed, if we take the side of the triangle to be $1$ , $P_2A + P_2B + P_2C = 1 + \frac{\sqrt{3}}{2}$ and $OA + OB + OC = \sqrt{3}$ ).

$\mathbf{Proof\ of\ 3:}$ Assume that $P$ is inside the triangle $\triangle ABC$ . In this case, we make a proof by contradiction. We will show that if $P$ is a point where $PA + PB + PC$ is minimum, then the extensions of $PA, PB, PC$ are perpendicular to the opposite sides $BC, AC, AB$ . (This statement implies that $P = O$ .) If this were not true, at least one of $PA \perp BC, PB \perp AC, PC \perp AB$ would be false. We can assume that $PC$ is not perpendicular to $AB$ . Then draw the ellipse with focal points $A, B$ which goes through $P$ .

Now consider the point $P_1$ on the ellipse such that $CP_1 \perp AB$ . Because of the properties of the ellipse, $CP_1 < CP$ , and because of the definition of the ellipse $PA + PB = P_1A + P_1B$ . We conclude that $PA + PB + PC > P_1A + P_1B + P_1C$ , which contradicts the assumption that $P$ was such that $PA + PB + PC$ was minimum.

This proves the 2-dimensional case.

NOTE: a very picky reader might object that the proof used that a minimum of $PA + PB + PC$ exists, and is achieved at a point $P$ inside the triangle. This can be justified simply by noting that $PA + PB + PC > 0$ and quoting the theorem from calculus (or is it topology?) which says that a continuous function on a closed, bounded set has a minimum, and there is a point where the minimum is achieved. Because of the arguments in the proof, this point can not be on the boundary of the triangle, so it is inside.

Now we will give the proof in the 3-dimensional case. We will do the proof in three steps. It is extremely similar to the proof in the 2-dimensional case, we just need to go from 2D to 3D, so I will skip some details.

$\mathbf{1.}$ We will show that if $P$ is in one of the exterior regions, then there is a point $P_!$ on the boundary of the tetrahedron (a vertex, or on a edge, or on a side, such that $PA + PB + PC + PD > P_1A + P_1B + P_1C + P_1D$ .

$\mathbf{2.}$ Then we will show that if $P$ is on the boundary, then $PA + PB + PC + PD > OA + OB + OC + OD$ .

$\mathbf{3.}$ For the final step, consider the plane going through the edge $CD$ perpendicular to the edge $AB$ , the plane going through $AB$ perpendicular to $CD$ , the plane going through $CA$ perpendicular to $BD$ , etc. There are six such planes, and they all contain $O$ , the center of the circumscribed sphere. We will show that if $P$ is a point of minimum for $PA + PB + PC + PD$ inside the tetrahedron, then $P$ is in each of the six planes described above. This implies that $P = O$ .

$\mathbf{Proof\ of\ 1:}$ Let $P$ be in one of the exterior regions. Assume $P$ is in a prism shaped region delimited by extensions of three sides meeting in a vertex (there are 4 of them). Assume it is at vertex $A$ , the sides being the extensions of planes $ABC, ABD, ACD$ . Then take $P_1 = A$ . We have $PA + PB + PC + PD > P_1A + P_1B + P_1C + P_1D$ because of obtuse triangles formed with $PP_1$ .

Now assume $P$ is in one of the wedge shaped regions, formed by an edge and the extensions of two sides going through them. (there are six such regions.) Assume this is the line $AB$ and the extensions of $ABC, ABD$ . Then take $P_1$ to be the foot of the perpendicular from $P$ to $AB$ . Again, we have the desired inequality because $PP_1$ formed some right and obtuse triangles.

Now assume $P$ is in the truncated prism region delimited by a side and the extensions of the faces going through the edges of this side. (There are four such regions.) Assume this is the side $ABC$ , and extensions of the sides $DAB, DBC, DCA$ . Then take $P_1$ to be the foot of the perpendicular from $P$ to the plane $ABC$ . Again, we have the desired inequality because of right and obtuse triangles formed by $PP_1$ .

$\mathbf{Proof\ of\ 2:}$ Assume $P_1 = A$ . If we take the edge of the tetrahedron to be $1$ , a direct computation gives us that $P_1A + P_1B + P_1C + P_1D = 3$ , and $OA + OB + OC + OD = 4 \cdot \frac{\sqrt{6}}{4} = \sqrt{6}$ .

Assume $P_1$ is on $AB$ . If $P_1$ is not the midpoint of $AB$ , take $P_2$ to be the midpoint of $AB$ . Then $P_1A + P_1B + P_1C + P_1D > P_2A + P_2B + P_2C + P_2D$ because of right triangles formed by $P_2C, P_2D$ . And, if we take the edge of the tetrahedron to be $1$ , a direct computation yields that $P_2A + P_2B + P_2C + P_2D = 1 + 2 \cdot \frac{\sqrt{3}}{2} = 1 + \sqrt{3}$ , which is bigger than $OA + OB + OC + OD = \sqrt{6}$ .

Assume $P_1$ is on $ABC$ . If $P_1$ is not the circumcenter of $\triangle ABC$ then take $P_2$ to be the circumcenter. We have $P_1D > P_2D$ because $P_2D \perp ABC$ . We also have $P_1A + P_1B + P_1C > P_2A + P_2B + P_2C$ because we proved the 2-dimensional analogue of the problem. And, if we take the edge of the tetrahedron to be $1$ , we have $P_2A + P_2B + P_2C + P_2D = \sqrt{3} + \frac{\sqrt{6}}{3}$ , which is bigger than $OA + OB + OC + OD = \sqrt{6}$ .

NOTE: In the above paragraph, we used that the similar result is true in the 2-dimensional case, with an equilateral triangle instead of a regular tetrahedron.

NOTE: This part of the proof concludes filling in the gap in the first "Solution", written above. (A reader may complain that the proof in Solution 2 is very long (compared to the first "Solution"), but the first "Solution" should have done this too, one way or another.)

$\mathbf{Proof\ of\ 3:}$ Now consider the six planes going through one edge, perpendicular to the opposite edge. They intersect at the circumcenter of the tetrahedron. Assume $P$ is a point in the interior of the tetrahedron where $PA + PB + PC + PD$ achieves its minimum value. Then $P$ is in each of the six plane.

Prove this statement by contradiction. Assume that there is a plane among the six, so that $P$ is not on it. Assume the plane is the one going through $CD$ , perpendicular to $AB$ . To make it more explicit, this is the plane going through $C, D, E$ , where $E$ is the midpoint of $AB$ .

Consider the ellipsoid with focal points $A, B$ going through $P$ . This can be obtained as the set of points $Q$ in space so that $QA + QB = PA + PB$ . It can also be obtained as the surface obtained when we form the ellipse with focal points $A, B$ in the plane $ABC$ (as the set of points $Q$ so that $QA + QB = PA + PB$ ), and we rotate this ellipse from the plane $ABC$ around its axis $AB$ . Let $P_1$ be the foot of the perpendicular from $P$ to the plane $CDE$ . We have $PC > P_1C, PD > P_1D$ because $PP_1 \perp CDE$ . We also have $PA + PB > P_1A + P_1B$ because $P_1$ is in the interior of the ellipsoid. (Indeed, the intersection of the plane $CDE$ and the ellipsoid is the circle generated by rotating the ends of the small axis of the ellipse in the plane $ABC$ . Since the point $P$ is not on the plane CDE, it must be on a smaller circle, so its projection to the plane $CDE$ will be inside.)

This concludes the proof of the problem.

[Solution by pf02, September 2024]

1966 IMO (Problems) • Resources
Preceded by Problem 2	1 • 2 • 3 • 4 • 5 • 6	Followed by Problem 4
All IMO Problems and Solutions

Page

Toolbox

Search