Mock AIME 3 Pre 2005 Problems/Problem 14: Difference between revisions

Latest revision as of 01:05, 25 November 2023

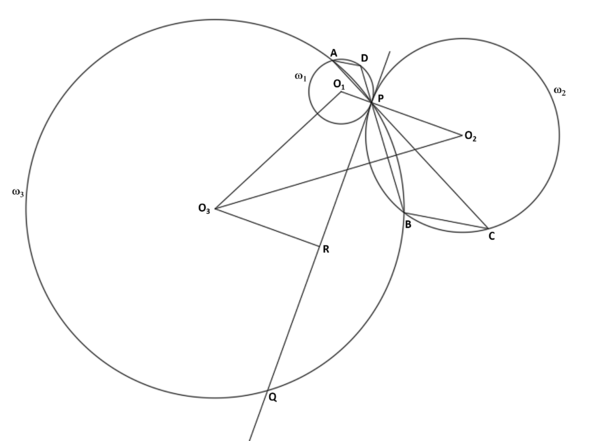
Problem

Circles $\omega_1$ and $\omega_2$ are centered on opposite sides of line $l$ , and are both tangent to $l$ at $P$ . $\omega_3$ passes through $P$ , intersecting $l$ again at $Q$ . Let $A$ and $B$ be the intersections of $\omega_1$ and $\omega_3$ , and $\omega_2$ and $\omega_3$ respectively. $AP$ and $BP$ are extended past $P$ and intersect $\omega_2$ and $\omega_1$ at $C$ and $D$ respectively. If $AD = 3, AP = 6, DP = 4,$ and $PQ = 32$ , then the area of triangle $PBC$ can be expressed as $\frac{p\sqrt{q}}{r}$ , where $p, q,$ and $r$ are positive integers such that $p$ and $r$ are coprime and $q$ is not divisible by the square of any prime. Determine $p + q + r$ .

Solution

Let $O_1, O_2,$ and $O_3$ be the centers of $\omega_1, \omega_2$ and $\omega_3$ respectively.

Let point $R$ be the midpoint of $QP$ . Thus, $O_3R \bot PQ$ and $|PR|=\frac{|PQ|}{2}=16$

Let $r_1$ and $r_2$ be the radii of circles $\omega_1$ and $\omega_2$ respectively.

Let $A_1$ and $A_2$ be the areas of triangles $PDA$ and $PBC$ respectively.

Since $O_3R \parallel O_1O_2$ and $\angle RO_3O_2 = \angle O_3O_2O_1$ , then $O_2B \parallel O_1D$ , and $BC \parallel AD$

This means that $\Delta PDA \sim \Delta PBC \sim \Delta O_3O_1O_1$ . In other words, those three triangles are similar.

Since $r_1$ is the circumcenter of $\Delta PDA$ ,

then $r_1=\frac{|AD| \times |DP| \times |AP|}{4A_1}=\frac{(3)(4)(6)}{4A_1}=\frac{18}{A_1}$

Let $h_1$ be the height of $\Delta PDA$ to side $AD$

Then, $A_1=\frac{|AD| \times h_1}{2}$ , thus $h_1=\frac{2}{3}A_1$

Since $PR$ is the height of $\Delta O_1O_2O_3$ to side $O_1O_2$ , then using similar triangles,

$\frac{|O_1O_2|}{|PR|}=\frac{|AD|}{h_1}$ . Therefore, $\frac{r_1+r_2}{16}=\frac{3}{\frac{2}{3}A_1}$ . Solving for $r_2$ we have:

$r_2=\frac{72}{A_1}-r_1=\frac{72}{A_1}-\frac{18}{A_1}=\frac{54}{A_1}=3\left( \frac{18}{A_1} \right)=3r_1$

By similar triangles,

$A_2=\left( \frac{r_2}{r_1} \right)^2A_1=9A_1$

Using Heron's formula,

$A_1=\sqrt{s(s-a)(s-b)(s-c)}$ , where $s=\frac{a+b+c}{2}=\frac{3+6+4}{2}=\frac{13}{2}$ we have:

$A_1=\sqrt{\left( \frac{13}{2} \right)\left( \frac{13}{2}-3\right)\left( \frac{13}{2}-6 \right)\left( \frac{13}{2}-4 \right)}$

$A_1=\frac{\sqrt{\left(13\right)\left(7\right)\left(1\right)\left(5\right)}}{4}=\frac{\sqrt{455}}{4}$

$A_2=9A_1=\frac{9\sqrt{455}}{4}=\frac{p\sqrt{q}}{r}$ , thus $p=9,q=455,r=4$

$p+q+r=\boxed{468}$

~Tomas Diaz. orders@tomasdiaz.com

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

@@ Line 28: / Line 28: @@
 Since <math>PR</math> is the height of <math>\Delta O_1O_2O_3</math> to side <math>O_1O_2</math>, then using similar triangles,
-<math>\frac{|O_1O_2|}{|PR|}=\frac{|AD|}{|h_1|}</math>. Therefore, <math>\frac{r_1+r_2}{16}=\frac{3}{\frac{2}{3}A_1}</math>.  Solving for <math>r_2</math> we have:
+<math>\frac{|O_1O_2|}{|PR|}=\frac{|AD|}{h_1}</math>. Therefore, <math>\frac{r_1+r_2}{16}=\frac{3}{\frac{2}{3}A_1}</math>.  Solving for <math>r_2</math> we have:
 <math>r_2=\frac{72}{A_1}-r_1=\frac{72}{A_1}-\frac{18}{A_1}=\frac{54}{A_1}=3\left( \frac{18}{A_1} \right)=3r_1</math>

Mock AIME 3 Pre 2005 (Problems, Source)
Preceded by Problem 13	Followed by Problem 15
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15

Page

Toolbox

Search

Mock AIME 3 Pre 2005 Problems/Problem 14: Difference between revisions

Latest revision as of 01:05, 25 November 2023

Problem

Solution

See Also