Art of Problem Solving
Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

2021 JMPSC Sprint Problems/Problem 16: Difference between revisions

← Older edit
Samrocksnature (talk | contribs)
editor
449 edits
No edit summary
Kante314 (talk | contribs)
editor
67 edits
No edit summary
 
(One intermediate revision by one other user not shown)
Line 11: Line 11:
~Mathdreams
~Mathdreams


== Solution 2 ==
<cmath>[ACD] = \frac{24 \cdot 20}{2}=240</cmath>
<cmath>[ABC] = \frac{12 \cdot 16}{2}=96</cmath>
Therefore, <math>[ABCD] = 240-96=144</math>


- kante314 -


==See also==
==See also==

Latest revision as of 09:39, 12 July 2021

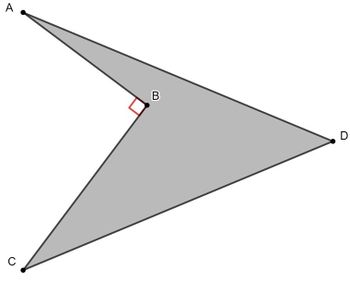
Problem

$ABCD$ is a concave quadrilateral with $AB = 12$, $BC = 16$, $AD = CD = 26$, and $\angle ABC=90^\circ$. Find the area of $ABCD$.

Solution

Notice that $[ABCD] = [ADC] - [ABC]$ and $AC = \sqrt{12^2 + 16^2} = 20$ by the Pythagorean Thereom. We then have that the area of triangle of $ADC$ is $\frac{20 \cdot \sqrt{26^2 - 10^2}}{2} = 240$, and the area of triangle $ABC$ is $\frac{12 \cdot 16}{2} = 96$, so the area of quadrilateral $ABCD$ is $240 - 96 = 144$.

~Mathdreams

Solution 2

\[[ACD] = \frac{24 \cdot 20}{2}=240\] \[[ABC] = \frac{12 \cdot 16}{2}=96\] Therefore, $[ABCD] = 240-96=144$

- kante314 -

See also

  1. Other 2021 JMPSC Sprint Problems
  2. 2021 JMPSC Sprint Answer Key
  3. All JMPSC Problems and Solutions

The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition.

Retrieved from "https://wiki.aopstest.com/wiki/index.php?title=2021_JMPSC_Sprint_Problems/Problem_16&oldid=158214"